How many edges?

Geometry Level 1

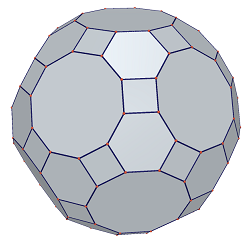
This is the great rhombicosidodecahedron.

It has 62 faces and 120 vertices.

How many edges does it have?

The answer is 180.

2 solutions

Geoff Pilling
Dec 21, 2016

Define the following:

$E =$ Number of Edges
$V =$ Number of Vertices
$F =$ Number of Faces

Using Euler's formula:

$V-E+F=2$

$E = V+F-2 = 120+62-2 = \boxed{180}$

Did not remember that formula, but the visual helped to show that every vertex is a junction of 3 edges, each being shared by 2 faces, so 120*3/2=180 is the answer I am looking for.

Saya Suka - 4 years, 5 months ago

I reminded myself of Euler's formula by thinking of a cube and remembering there's a 2 involved somewhere, but I like your approach Saya.

In case anybody tried it, there are 12 decagons, 20 hexagons and 30 squares.

This makes the number of edges $\frac{12 \times 10 + 20 \times 6 + 30 \times 4}{2} = 180$ faces, dividing by 2 because every edge is the meeting of two faces..

Interesting that $12 \times 10 = 20 \times 6 = 30 \times 4 = 120$ . Is there a reason for that?

Paul Hindess - 4 years, 5 months ago

Interesting observation, Paul... This seems to be true for three other Archimedean solids as well:

cuboctahedron (8 triangles, 6 squares)
truncated cuboctahedron (12 squares, 8 hexagons, 6 octagons)
icosidodecahedron (20 triangles, 12 pentagons)

Geoff Pilling - 4 years, 5 months ago

Keshav Ramesh
Feb 5, 2017

Since Euler's Polyhedral Formula is F+V=E+2 where F=Faces, V=Vertices, and E=Edges, we have that 62+120=E+2.

This can simplify to: 62+120=E+2 182=E+2 E=182-2 E=180

Therefore, this rhombicosidodecahedron has 180 edges.

How many edges?

The answer is 180.

2 solutions

0 pending reports