How many Happy triangles?

Level pending

How many distinct equilateral triangles can we count in the diagram below such that

  1. every vertex of the triangle is a vertex on the diagram, and
  2. the triangle is oriented in the same direction as triangle A B C ? ABC?

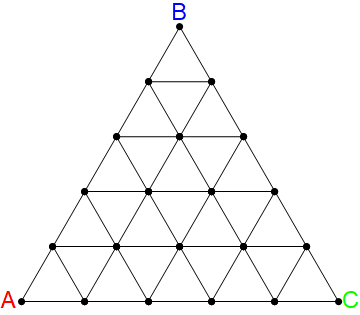
Bonus and Details:

  • What's the general formula for the corresponding question with the diagram having n n rows in the triangular grid?
  • This is not an original question from me.


The answer is 35.

Roberto Nicolaides by Roberto Nicolaides , 26, United Kingdom

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

In general, the formula for ABC having side length n (assuming the length of an edge between adjacent vertices in the diagram is length 1) gives ( n + 2 3 ) n+2 \choose 3 . Here is a quick animation to try help see why this is true.

Here is a note going into more detail of how it works.

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...