How many ice cubes?

My "markup language": V- the volume of one ice cube, N- the number of ice cubes, w=water and i=ice.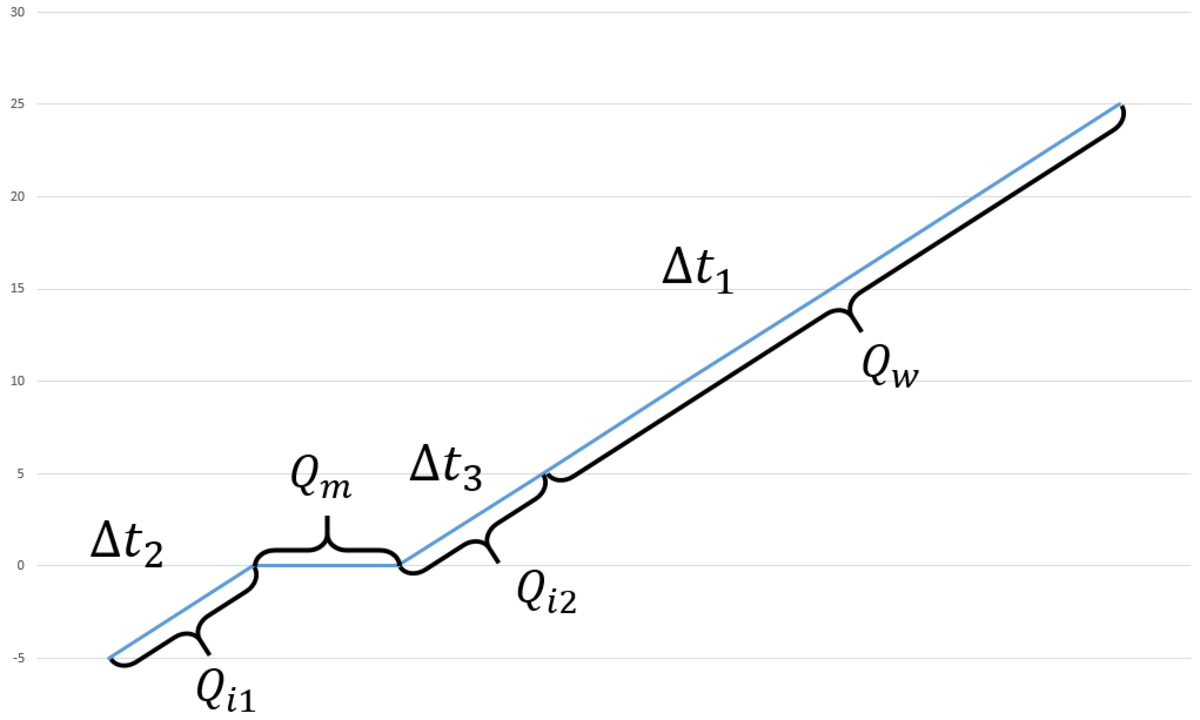 In this picture you can see the processes

$Q_w=Q_{i1}+Q_{i2}+Q_m$ $c_wm_w\Delta t_1=c_im_i\Delta t_2+c_wm_i\Delta t_3+L_im_i$ $c_wm_w\Delta t_1=m_i(c_i\Delta t_2+c_w\Delta t_3+L_i)$ $\frac{c_wm_w\Delta t_1}{c_i\Delta t_2+c_w\Delta t_3+L_i}=m_i$ $\rho _iV_i=\frac{c_wm_w\Delta t_1}{c_i\Delta t_2+c_w\Delta t_3+L_i}$ $\rho _iVN=\frac{c_wm_w\Delta t_1}{c_i\Delta t_2+c_w\Delta t_3+L_i}$ $N=\frac{c_wm_w\Delta t_1}{\rho _iV(c_i\Delta t_2+c_w\Delta t_3+L_i)}$ $N=\frac{4200\cdot 0.2\cdot 20}{900\cdot 6.4\cdot 10^{-6}(2100\cdot 5+4200\cdot 5+3.3\cdot 10^5)}$ $N=\frac{16800}{5,76\cdot 10^{-3}\cdot 361500}\approx 8$

P.S. $N^{\circ}1$ If somebody want to say $N>8$ : $L_i=3.334\cdot 10^5\frac{J}{kg}$ , therefore $N<8$ .
P.S. $N^{\circ}2$ I doubt anyone likes to read Soviet books, but I would like note that in the book the solution is 9. I think this is only a typo.