How many Integer Solutions?

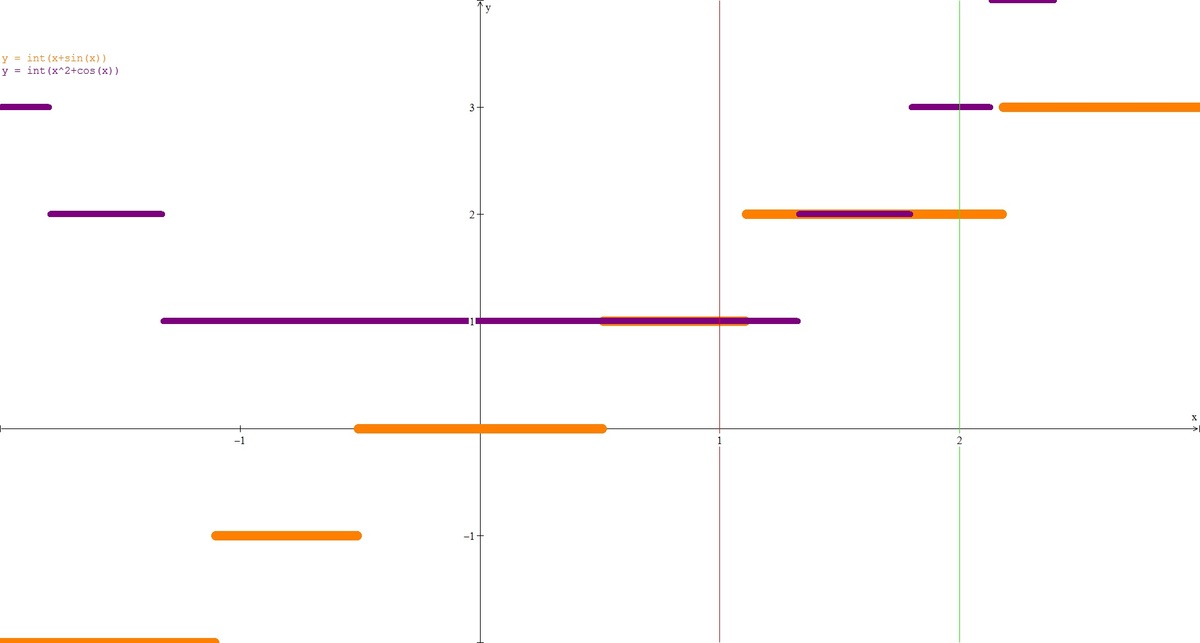
We note that for integer $x$ : $\quad \begin{cases} \text{For } x = 0: & \sin x = 0, & \cos x = 1 \\ \text{For } x \ne 0: & 0 < |\sin x| < 1, & 0 < |\cos x| < 1 \end{cases}$

$\implies$ For $x = 0$ : $\quad \begin{cases} \lfloor x + \sin x \rfloor = 0 \\ \lfloor x^2 + \cos x \rfloor = 1 \end{cases} \implies$ LHS $\ne$ RHS.

$\implies$ For $x \ne 0$ : $\quad \begin{cases} \lfloor x + \sin x \rfloor = \begin{cases} x & \text{if }\sin x > 0 \\ x-1 & \text{if }\sin x < 0 \end{cases} \\ \lfloor x^2 + \cos x \rfloor = \begin{cases} x^2 & \text{if }\cos x > 0 \\ x^2-1 & \text{if }\cos x < 0 \end{cases} \end{cases}$

Let's check the four cases:

1. $x = x^2 \implies x = 1$ and since $\sin 1 > 0$ and $\cos 1 > 0$ , the equality is true .
2. $x = x^2 - 1 \implies x^2 - x -1=0$ ; there is no integer root.
3. $x-1 = x^2 \implies x^2 - x + 1 = 0$ ; there is no real root.
4. $x-1 = x^2 -1 \implies x = x^2$ same as case 1.

Therefore, there is only $\boxed{1}$ integer solution, when $x=1$ .

The only Integer solution is $x=1$ . Therefore, the answer is $\boxed {1}$ .

If $x$ is allowed to be a Real number, then there are infinitely many solutions.

Outside the interval ${[-1,3]}$ the graphs of the LHS and RHS separate widely.

Only integer 1 is 1=1 1 since there is x and x x. So only one solution. Sin(1) will vanish since we talk of floor.