How many little hexagons in the figure?
This problem's question: How many little hexagons in the figure?
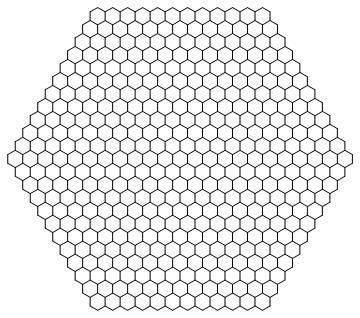
This problem is extremely easy. You can just count the little hexagons. You could note some regularities and reduce the problem to a small arithmetic problem. You could find or even develop the polynomial to compute the appropriate number for a given .
Somehow the figure was not included before initial posting! I regret that event.
The answer is 397.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
If you exclude the center hexagon, then remainder of the figure can be divided into 6 triangle with a base one less the edge count of the large hexagon. This directly gives a polynomial for computing the count for a given edge count n : 1 + 6 ( 2 n ( n − 1 ) ) . Using n = 1 2 in that polynomial , the result is 397.