How many methods for this?
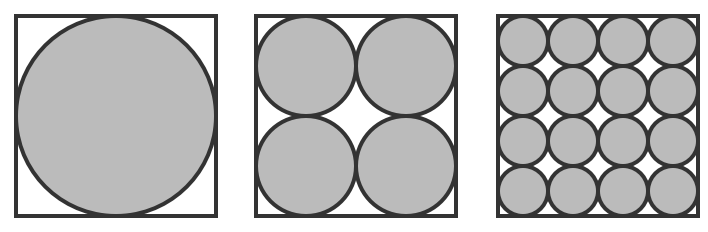
Each square has equal area. What can you say about the shaded region in each square?
Note : In a square, each circle have same radii.
- Inspired by Arron Kau's set
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
In all three pictures the same geometric shape is used, this means that we can solve it just by thinking about percentage areas.
In the largest image we can think about the area taken up by the gray circle as a percentage of total area of the square. Lets call this percentage n %
Note that it doesn't matter what scale the circle and square are in, as long as it is in the same proportions the grey circle will still occupy n % of the space. (you can prove this easily with a little geometry).
Hence when we scale down our largest title so that it's edges are 1/2 the original length (see the second image) - each circle takes up n % of its respective square.
Now to work out the percentage of the area of the larger square (in the second image) that is shaded grey we just need to take the percentage that is shaded grey for each constituent element and times in by the fraction of the total area that it takes up. In this case this yields 4 n % per square, which gives 4 n × 4 = n %
You can repeat this for the third.
Not quite as clean as a mathematical proof, but makes for a nice little thought experiment
Let's assume that the length of one side of the square is 1. Area with 1 shaded = pi(1)^2 = pi, area w/ 16 shaded region is (16)(pi(1/4)^2) = pi, and area w/ 4 shaded regions is (4)(pi(1/2)^2) = pi . .thus they are all equal
If we held R constant, since if you add the radii of either dimension, you'd get the same for each diagrams. And setting R = a r then A r e a t o t a l = n π ( a r ) 2 where n = number of circles and a = average number of circles per row or column. The only way the areas to be equal is where n = a 2 and since it's enclosed by a square. then a r o w = a c o l u m n and n = a r o w a c o l u m n so, n = a 2 Thus, the area is the same for all values of a > 0
If radius of each circle is same, then area is also same. Area is propotional to square of radius.
let radius of smallest circle be r then shaded area of 3rd square is 16 3.14 r^2 then radius of circle of 2nd square is 2r since all the square are same then the shaded area of 2nd square is 4 3.14 (2r)^2=4 3.14 4 r^2=16 3.14 r^2 then radius of circle of 1st square is 4r then shaded area = 3.14 (4r)^2=3.14 16 r^2 therefore, shaded area of 1st square= shaded area of 2nd square = shaded area of 3rd area
Assume Radius of third square= r 3
Radius of second square= r 2 = 2 r 3
Radius of first square= r 1 = 4 r 3
As a result π ( r 1 ) 2 = π ( 4 r 3 ) 2 = 4 π ( 2 r 3 ) 2 = 1 6 π ( r 3 ) 2