How many pages? (2)

From $1 - 99$ ,

There are $90$ 2-digit numbers, total $90\times 2 = 180$ digits.

deduct $9$ '0' from the $180$ digits, every non-zero digit appears $= 171 \div 9 = 19$ times

$\therefore$ every non-zero digit appears $\color{#3D99F6} 19+1 = 20$ times,

'0' digit appears $\color{#3D99F6}9$ times.

Total $= 189$ digits.

From $\overline{a00} - \overline{a99}$ ,

Every non-zero digit not equal $a$ appears $\color{#3D99F6}20$ times,

'a' digit appears $\color{#3D99F6}= 100 + 20 = 120$ times,

'0' digit appears $\color{#3D99F6}= 2 (00) + 9 (01-09) + 9 (10-99) = 20$ times

Total $= 300$ digits.

From $\overline{a00} - \overline{a09}$ ,

Every non-zero digit not equal $a$ appears $\color{#3D99F6}1$ times,

'a' digit appears $\color{#3D99F6}= 10 + 1 = 11$ times,

'0' digit appears $\color{#3D99F6}= 2 + 9 = 11$ times.

Total $= 30$ digits.

From $\overline{ab0} - \overline{ab9}$ ,

Every non-zero digit not equal $a, b$ appears $\color{#3D99F6}1$ times,

'a' digit appears $\color{#3D99F6}= 10 + 1 = 11$ times,

'b' digit appears $\color{#3D99F6}= 10 + 1 = 11$ times,

If a=b, a digit appears $\color{#3D99F6}= 10+10+1 = 21$ times

'0' digit appears $\color{#3D99F6}= 1$ times.

Total $= 30$ digits.

The digit $3$ appears $87$ times, $87 = 20 + 20 + 20 + 11 + 11 + 5\implies$ the book has $323$ pages.

For the number $3$ to appear exactly $87$ times, we need exactly $323$ pages.

The page numbers having $3$ are as follows:

$3, 13, 23, 30, 31, 32, 33 (2$ times) $, 34, 35, 36, 37, 38, 39, 43, 53, 63, 73, 83, 93, 103, 113, 123, 130, 131, 132, 133 (2$ times $), 134, 135, 136, 137, 138, 139, 143,$

$153, 163, 173, 183, 193, 203, 213, 223, 230, 231, 232, 233 (2$ times $), 234, 235, 236, 237, 238, 239, 243, 253, 263, 273, 283, 293, 300, 301, 302,$

$303 (2$ times $), 304, 305, 306, 307, 308, 309, 310, 311, 312, 313 (2$ times $), 314, 315, 316, 317, 318, 319, 320, 321, 322, 323 (2$ times $)$ .

Hence, the total number of $3$ s are $87$ .

I have got the answer through a Python program built in the coding environment of brilliant

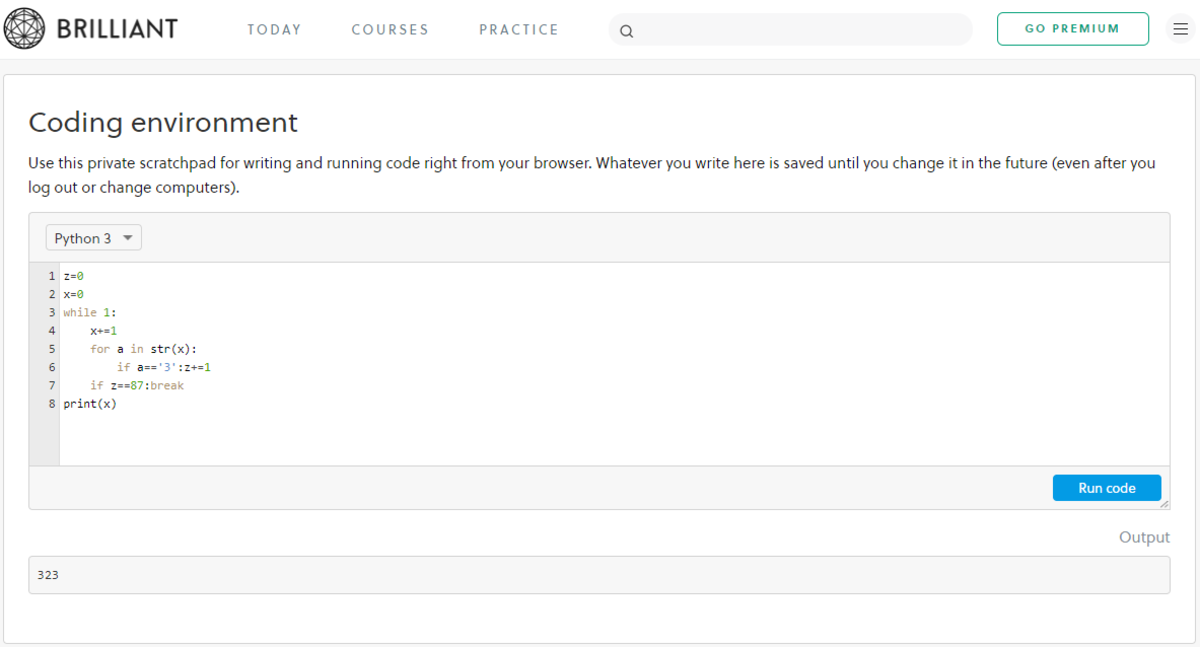
3,13,23,30,31,32,33(2 times), 34, 35, 36, 37, 38, 39, 43, 53, 63, 73, 83, 93, 103, 113, 123, 130, 131, 132, 133,(2 times), 134, 135, 136, 137, 138, 139, 143,134,135,136,137,138,139,143,

153, 163, 173, 183, 193, 203, 213, 223, 230, 231, 232, 233,(2 times), 234, 235, 236, 237, 238, 239, 243, 253, 263, 273, 283, 293, 300, 301, 302,),234,235,236,237,238,239,243,253,263,273,283,293,300,301,302,

303 (2 times), 304, 305, 306, 307, 308, 309, 310, 311, 312, 313,(2 times), 314, 315, 316, 317, 318, 319, 320, 321, 322, 323 (2),314,315,316,317,318,319,320,321,322,323(2 times).

Hence, the total number of 3s are 87.

(this whole thing is copied from near by given solution because i can't write this whole stuff again, ya i have wrote this in my notebook, so i ain't did it again.)

The digit '3' appears 20 times on pages 1-99 (ten times in the units column and ten times in the tens column), another 20 times on pages 100-199, and another 20 times on pages 200-299. Thus a total of 60 times on pages 1-299.

It appears 11 times on pages 300-309 (ten times in the hundreds column and once in the units column) and another 11 times on pages 310-319. Running total is 82, leaving five to go: From pages 320-322 we see three 3's. And we reach 87 3's at 323. If we added another page another '3' would appear, so the only possibility is 323 pages.