How many rectangles can you make?
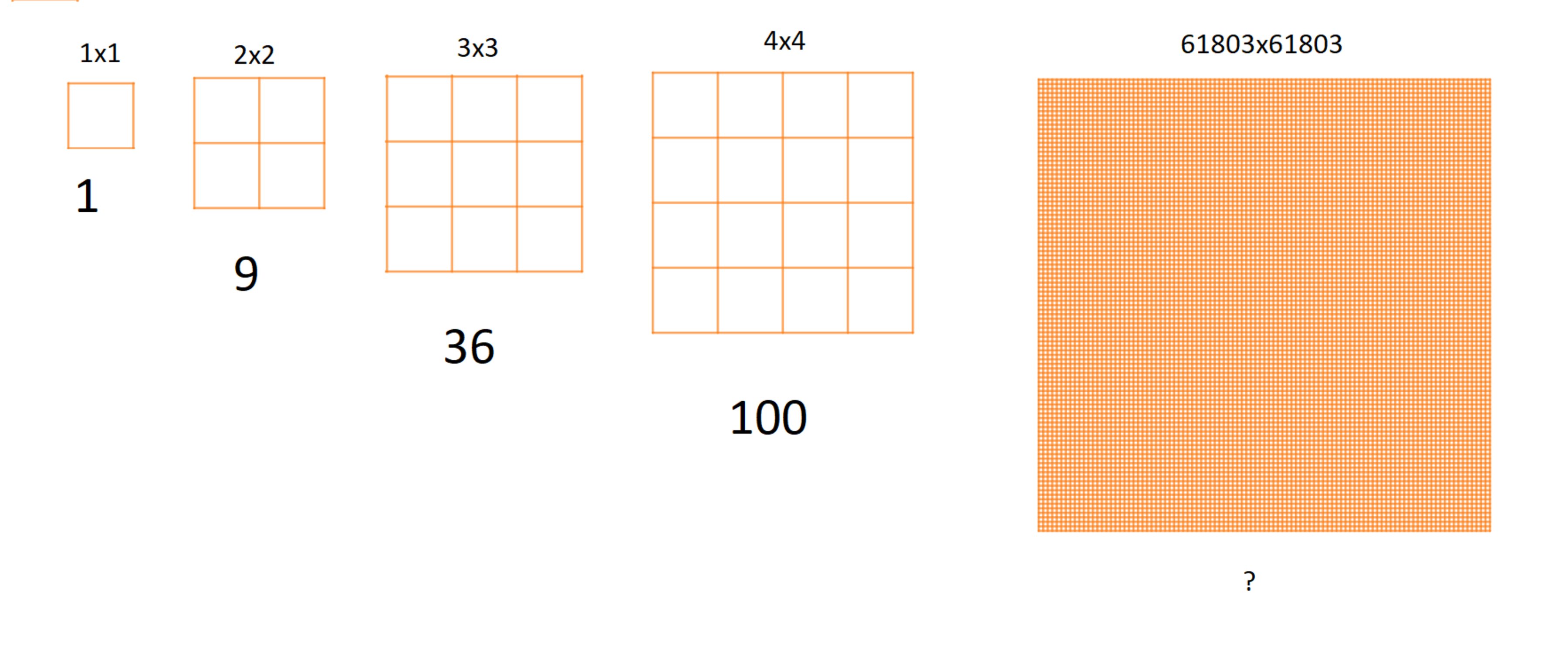
In an by grid, you can make different rectangles. The first few values of are given in the picture. (i.e. In a 1x1 grid, and ; In a 2x2 grid, and , etc)
If , what is the sum of the first and last digits of
Note: A square is also a rectangle.
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
There are many approaches to this problem.
Great explanation by RedpenBlackpen here: https://www.youtube.com/watch?v=Uq9OXC0Gzgw
Taking 2 ( 6 1 8 0 3 ) ( 6 1 8 0 4 ) we will get 1909836306
Squaring this, we will get a value that begins with 3 as the first two digits are within ( 1 8 , 2 0 ) (all of which results in 3 as the first digit 18000... = 3##... and 19999^2 = 3##... )
The last digit will be a 6 , as any number with 6 as it's last digit results in a final digit of 6 .
3 + 6 = 9