How many right triangles with integer sides are there?

Geometry Level 4

How many right triangles with integer sides are there where the area and perimeter of the triangle have the same numerical value?


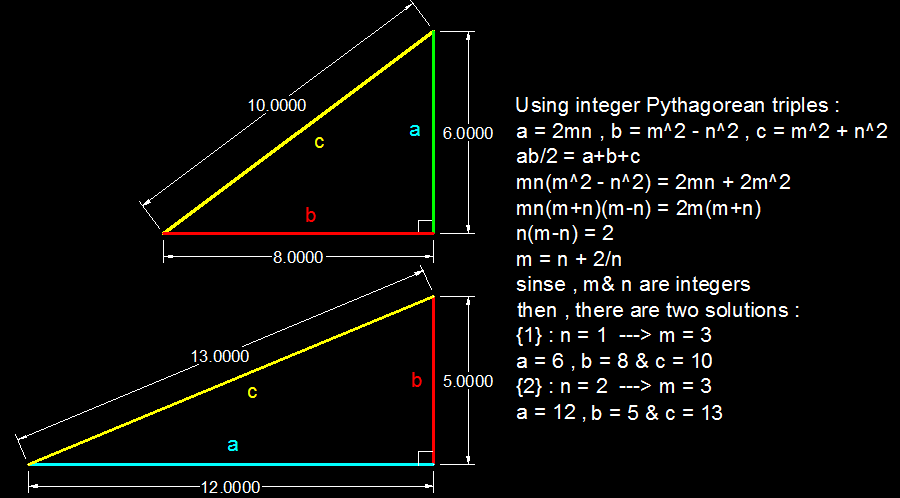
The answer is 2.

Vijay Simha by Vijay Simha , 47, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Ahmad Saad
Jun 11, 2016

3 Helpful 0 Interesting 0 Brilliant 0 Confused

Nice solution. I took a slightly different approach. I started with the condition equation

a b 2 = a + b + a 2 + b 2 ⟹ a b − 2 ( a + b ) = 2 a 2 + b 2 \dfrac{ab}{2} = a + b + \sqrt{a^{2} + b^{2}} \Longrightarrow ab - 2(a + b) = 2\sqrt{a^{2} + b^{2}} .

Squaring both sides gives us that

− 4 a b ( a + b ) + ( a b ) 2 + 4 ( a 2 + b 2 + 2 a b ) = 4 ( a 2 + b 2 ) ⟹ a b ( a b − 4 a − 4 b + 8 ) = 0 -4ab(a + b) + (ab)^{2} + 4(a^{2} + b^{2} + 2ab) = 4(a^{2} + b^{2}) \Longrightarrow ab(ab - 4a - 4b + 8) = 0 .

Since a b ≠ 0 ab \ne 0 we have that a b − 4 a − 4 b + 8 = 0 ⟹ ( a − 4 ) ( b − 4 ) = 8 ab - 4a - 4b + 8 = 0 \Longrightarrow (a - 4)(b - 4) = 8 .

Considering the factorizations of 8 8 we can have a − 4 = 1 , b − 4 = 8 ⟹ ( a , b , c ) = ( 5 , 12 , 13 ) a - 4 = 1, b - 4 = 8 \Longrightarrow (a,b,c) = (5,12,13) , or we can have a − 4 = 2 , b − 4 = 4 ⟹ ( a , b , c ) = ( 6 , 8 , 10 ) a - 4 = 2, b - 4 = 4 \Longrightarrow (a,b,c) = (6,8,10) .

Brian Charlesworth - 4 years, 10 months ago
Tom Engelsman
Jan 25, 2017

If the sides of the right triangle are x , y , x 2 + y 2 x, y, \sqrt{x^2 + y^2} ∈ N \in \mathbb{N} , then we wish to compute:

1 2 ⋅ x y = x + y + x 2 + y 2 \frac{1}{2} \cdot xy = x + y + \sqrt{x^2 + y^2} ;

or [ 1 2 ⋅ x y − ( x + y ) ] 2 = x 2 + y 2 ; [\frac{1}{2} \cdot xy - (x + y)]^{2} = x^{2} + y^{2};

or 1 4 ⋅ x 2 y 2 − x 2 y − x y 2 + x 2 + 2 x y + y 2 = x 2 + y 2 ; \frac{1}{4}\cdot x^{2}y^{2} - x^{2}y - xy^{2} + x^{2} + 2xy + y^{2} = x^{2} + y^{2};

or 1 4 ⋅ x 2 y 2 − x 2 y − x y 2 + 2 x y = 0 ; \frac{1}{4}\cdot x^{2}y^{2} - x^{2}y - xy^{2} + 2xy = 0;

or x y ( 1 4 ⋅ x y − x − y + 2 ) = 0. xy(\frac{1}{4}\cdot xy - x - y + 2) = 0.

In order for the above product to hold true, we require 1 4 ⋅ x y − x − y + 2 = 0 ⇒ y = 4 + 8 x − 4 \frac{1}{4}\cdot xy - x - y + 2 = 0 \Rightarrow y = 4 + \frac{8}{x - 4} . This requires the positive integer pairs: ( x , y ) = ( 5 , 12 ) ; ( 6 , 8 ) ; ( 8 , 6 ) ; ( 12 , 5 ) (x,y) = (5, 12); (6, 8); (8, 6); (12, 5) , which yields only the 5 − 12 − 13 \boxed{5-12-13} and the 6 − 8 − 10 \boxed{6-8-10} right triangles as solutions.

1 Helpful 0 Interesting 0 Brilliant 0 Confused

Examining Pythagorean triples, 3-4-5, 6-8-10, 5-12-13, 8-15-17, 9-12-15, we see 2nd and third ok. From the fourth the area is much more than the perimeter. So only two solutions. Here this method is much shorter than the use of theory.

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...