How Many Sides For Similarity?

Geometry Level 4

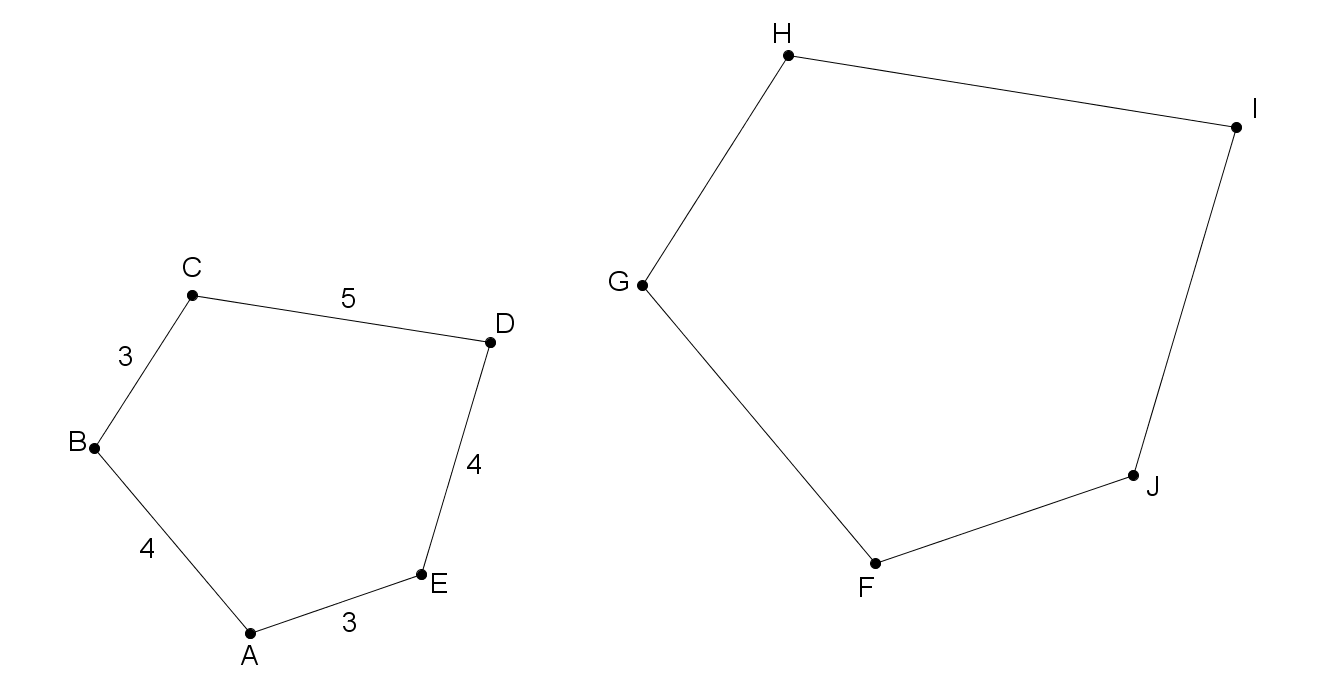
In the figure above, $\angle A\cong\angle F$ , $\angle B\cong\angle G$ , $\angle C\cong\angle H$ , $\angle D\cong\angle I$ , and $\angle E\cong\angle J$ .

You may set any side length in pentagon $FGHIJ$ to be whatever value you want. Your goal is to make the pentagons similar .

What is the minimum number of sides needed in order for both pentagons to always be similar?

0 1 2 3 4 5

1 solution

Andy Hayes
Apr 7, 2016

In order for the pentagons to be similar, all angles must be congruent and all sides must be proportional. The first requirement is already met in the problem description.

It is insufficient to prove that pentagons are similar if all corresponding angles are congruent. Below is a counterexample in which all corresponding angles are congruent, but not all sides are proportional:

Having one pair of sides be proportional is meaningless because it takes two pairs of sides to make a proportion. So far, we've eliminated the answer choices for $0$ and $1$ .

What if two adjacent sides in $FGHIJ$ are proportional to the corresponding sides in $ABCDE$ ? Look below:

The pentagons are not similar. How about two non-adjacent sides? Look below:

These pentagons are not similar either. Therefore, two sides is insufficient.

Now we'll try three adjacent sides in $FGHIJ$ proportional to the corresponding sides in $ABCDE$ .

This appears to work. To prove it, we'll divide the pentagons into triangles:

We can now prove that $ABCDE\sim FGHIJ$ .

1) $\angle B\cong\angle G$ and $\frac{FG}{AB}=\frac{GH}{BC}=\frac{3}{2}$ are given.

2) $\Delta ABC\sim\Delta FGH$ due to SAS similarity.

3) $\angle ACB\cong\angle FHG$ and $\frac{FH}{AC}=\frac{3}{2}$ because $\Delta ABC\sim\Delta FGH$

4) $\angle BCD\cong\angle GHI$ is given.

5) $\angle ACD\cong\angle FHI$ because $m\angle BCD-m\angle ACB=m\angle GHI-m\angle FHG$

6) $\Delta ACD\sim\Delta FHI$ due to SAS similarity.

7) $\angle ADC\cong\angle FIH$ and $\frac{FI}{AD}=\frac{3}{2}$ because $\Delta ACD\sim\Delta FHI$

8) $\angle CDE\cong\angle HIJ$ and $\angle E\cong\angle J$ are given.

9) $\angle ADE\cong\angle FIJ$ because $m\angle CDE-m\angle ADC=m\angle HIJ-m\angle FIH$

10) $\Delta ADE\sim\Delta FIJ$ due to AA similarity.

11) $\frac{FJ}{AE}=\frac{IJ}{DE}=\frac{FI}{AD}=\frac{3}{2}$ because $\Delta ADE\sim\Delta FIJ$ .

12) $ABCDE\sim FGHIJ$ because all angles are congruent and all sides are proportional.

I believe it is also possible to prove that three sides are sufficient even when one of the sides is not adjacent to the other two. I'll leave that for someone else to post!

Edit : It is not possible to prove. Simone provides a counter example, and I have a picture of that example below:

If 3 sides are proportional but not adjacents, it's not sufficient. As an example consider the pentagon formed by a square with a triangle on top (like a house): if you raise the ceiling, then you obtain two pentagons that are not similar, even if they have the same angles and 3 sides are congruents. Note that a similar condition holds for parallelograms: in order to be similar you need 2 adjacent sides to be proportional.

Simone Bertone - 5 years, 2 months ago

That's a great point! I had not considered an example with right angles. I included a picture of your example in my post.

Next challenge: Is it possible to prove similarity with three sides (one of which is non-adjacent) if the pentagons contain no right angles? Or maybe it has something to do with the line segments being parallel?

Andy Hayes - 5 years, 2 months ago

yes its possible $\huge\large\large{{{\color{#D61F06}{:D}}}}$

Syed Baqir - 5 years, 2 months ago

How Many Sides For Similarity?

1 solution

0 pending reports