Diophantine equation
How many solutions are there for the equation x 4 + 4 = p y 4 , where p is a prime, and x and y are integers?
It's a problem from a book written by Ion Cucurezeanu .
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
We may factorize the left-hand side using Sophie Germain to get ( x 2 + 2 x + 2 ) ( x 2 − 2 x + 2 ) = p y 4 . To exploit this factorization let's compute g cd ( x 2 + 2 x + 2 , x 2 − 2 x + 2 ) :
If d ∣ x 2 + 2 x + 2 , x 2 − 2 x + 2 ⟹ d ∣ 4 x , 2 x 2 + 4 ⟹ d ∣ 4 x 2 , 2 x 2 + 4 ⟹ d ∣ − 8 ⟹ d ∣ 8 . So g cd ( x 2 + 2 x + 2 , x 2 − 2 x + 2 ) ∣ 8 . We may now quickly examine two cases.
Case 1: y is even : Then y = 2 y 0 and thus x 4 + 4 = 1 6 p y 0 4 ⟹ x ≡ 0 m o d 2 ⟹ x = 2 x 0 ⟹ 1 6 x 0 4 + 4 = 1 6 p y 0 4 ⟹ 4 ≡ 0 m o d 1 6 . This is a contradiction so y must always be odd.
Case 2: p = 2 . If that is the case then x 4 + 4 = 2 y 4 ⟹ x ≡ 0 m o d 2 ⟹ x = 2 x 0 ⟹ 1 6 x 0 4 + 4 = 2 y 4 ⟹ 8 x 0 4 + 2 = y 4 ⟹ y ≡ 0 m o d 2 . This implies Case 1 which we know leads to a contradiction.
We now have that on the right-hand side of ( x 2 + 2 x + 2 ) ( x 2 − 2 x + 2 ) = p y 4 there are no even factors. This means that for each prime power on the right-hand side, all of it has to go to either of the two factors on the left. They cannot share factors (otherwise their gcd would not divide 8). Let's suppose that y = p 4 k y 0 4 . Then ( x 2 + 2 x + 2 ) ( x 2 − 2 x + 2 ) = p 4 k + 1 y 0 4 .
Case 1: x 2 + 2 x + 2 = p 4 k + 1 m 4 , x 2 − 2 x + 2 = n 4 . Focusing on x 2 − 2 x + 2 = n 4 , this implies that x 2 − 2 x + 2 − n 4 = 0 . This equation must have an integral discriminant so let's compute it: D = 2 2 − 4 ( 1 ) ( 2 − n 4 ) = 4 − 8 + 4 n 4 = ( 2 n 2 ) 2 − 4 . Using the substitution a = 2 n 2 , this would imply a solution to the equation a 2 − 4 = b 2 ⟹ a 2 − b 2 = 4 . To solve this simply examine the inequality a 2 − b 2 ≤ ( b + 1 ) 2 − b 2 = 2 b + 1 . And 2 b + 1 ≤ 4 ⟺ b ≤ 1 . Quickly checking, the only solution is a = 2 , b = 0 . So 2 n 2 = 2 ⟹ n 2 = 1 . Plugging this into the original polynomial equation we get x 2 − 2 x + 2 − 1 = 0 ⟹ ( x − 1 ) 2 = 0 ⟹ x = 1 . Plugging this into the other polynomial equation, 5 = p 4 k + 1 m 4 ⟹ p = 5 , k = 0 , m = ± 1 . Thus we have found the solution p = 5 , x = 1 , y = ± 1 .
Case 2: x 2 + 2 x + 2 = n 4 , x 2 − 2 x + 2 = p 4 k + 1 m 4 . It is easy to see that as the discriminants are the same, the previous case will repeat itself, only that now x = − 1 .
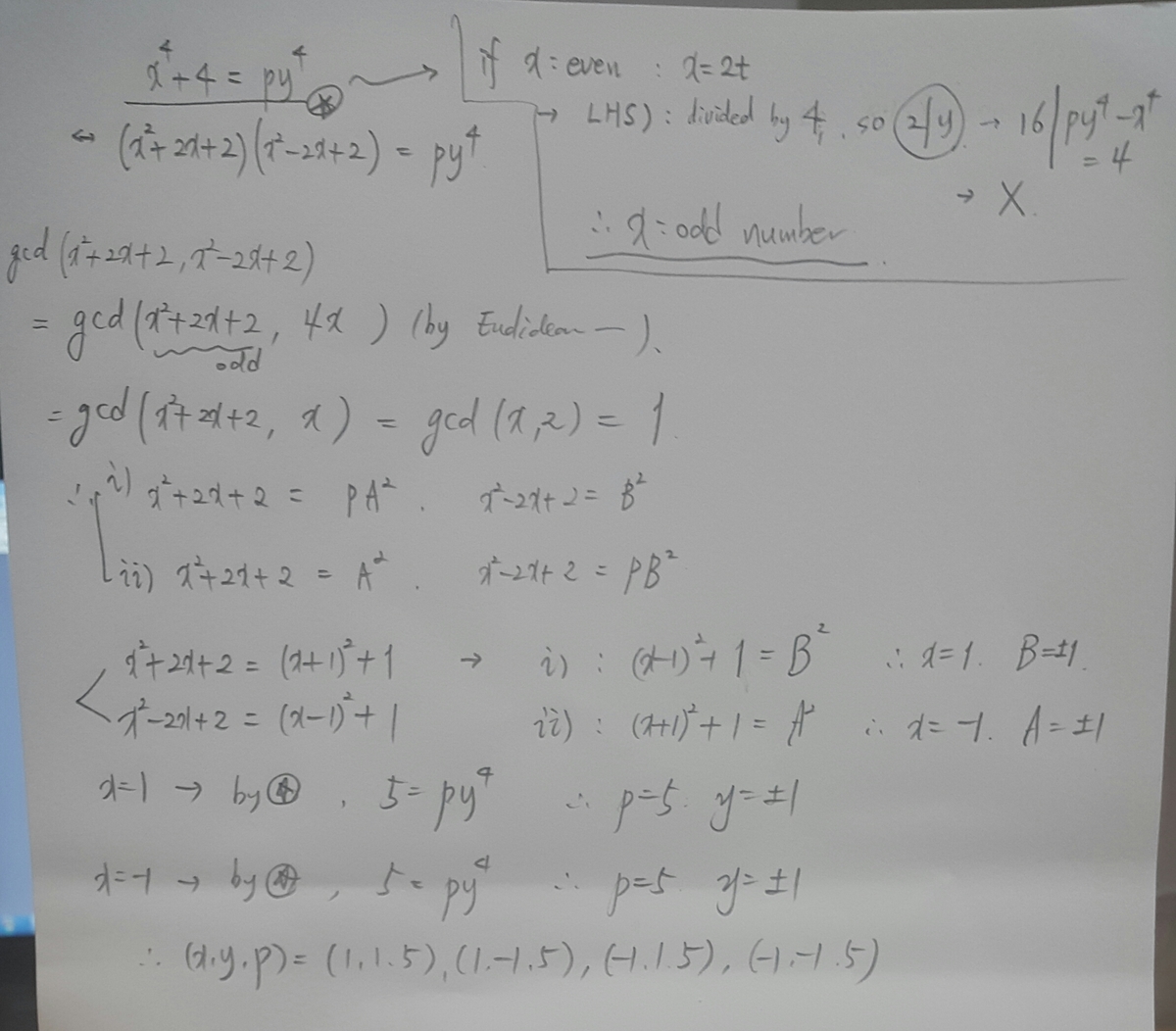 sorry, i can't use latex....T.T
sorry, i can't use latex....T.T