How Many Squares?
In the grid, there are squares with the side length of , squares with the side length of and square with the side length of , making squares totally.

How many squares are there in the grid?
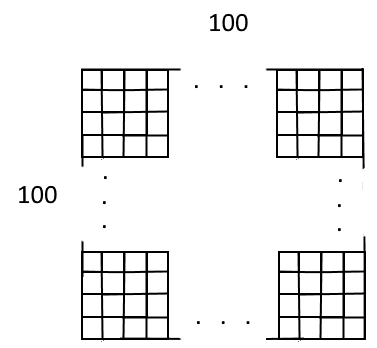
The answer is 338350.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
There are squares with side lengths k where 1 ≤ k ≤ 1 0 0 . With each side length k , there are ( 1 0 1 − k ) 2 possible unit squares to be the bottom left corner of the k × k square, as the picture below shows.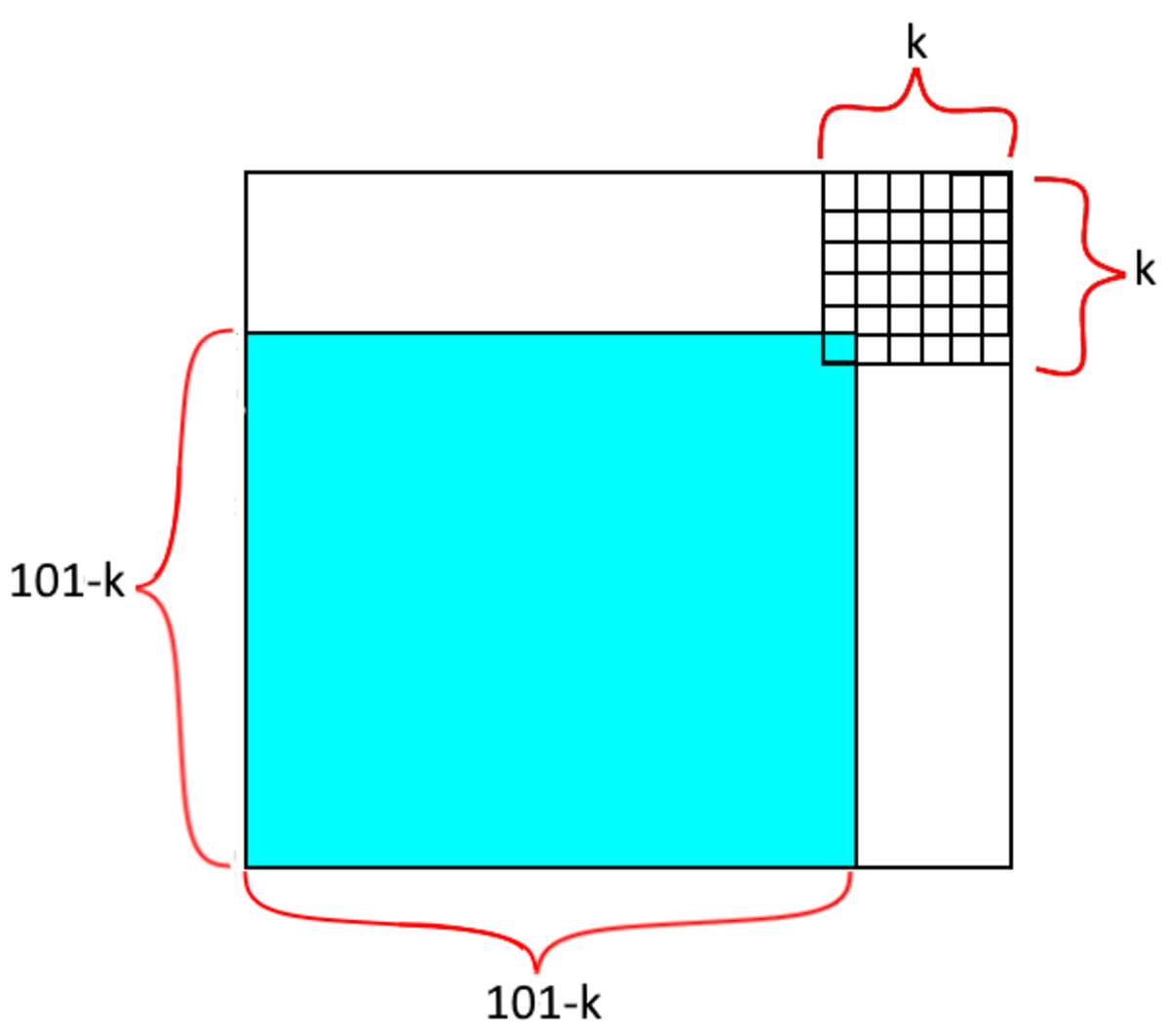
This means there are ( 1 0 1 − k ) 2 squares with any side length k and the total number of squares is k = 1 ∑ 1 0 0 ( 1 0 1 − k ) 2 = 1 0 0 2 + 9 9 2 + . . . + 2 2 + 1 2 = 1 2 + 2 2 + . . . + 9 9 2 + 1 0 0 2 = k = 1 ∑ 1 0 0 ( k 2 ) .
k = 1 ∑ 1 0 0 ( k 2 ) = k = 1 ∑ 1 0 0 ( 2 k × 2 k ) = k = 1 ∑ 1 0 0 ( 2 k ( 2 k + 2 ) − k ) = 2 k = 1 ∑ 1 0 0 ( 2 k ( k + 1 ) ) − k = 1 ∑ 1 0 0 ( k ) = k = 2 ∑ 1 0 1 ( 2 k ) − 2 1 0 0 ( 1 0 0 + 1 ) .
By Hockey Stick Identity, k = r ∑ n ( r k ) = ( r + 1 n + 1 ) .
We get
k = 2 ∑ 1 0 1 ( 2 k ) − 2 1 0 0 ( 1 0 0 + 1 ) = ( 3 1 0 2 ) − 5 0 5 0 = 3 4 3 4 0 0 − 5 0 5 0 = 3 3 8 3 5 0 .