How many squares on a grid
How many unique squares can be drawn inside a 16 x 16 square if their vertices must lie on a grid (lattice) of integer points? The sides of these smaller squares need not be parallel to the sides of the large square. Any vertex or edge on the boundary of the large square is counted as inside the large square. Bonus: can you generalize this to an n x n square?
Note: This is not a packing problem. These squares can overlap. How many such squares are there?
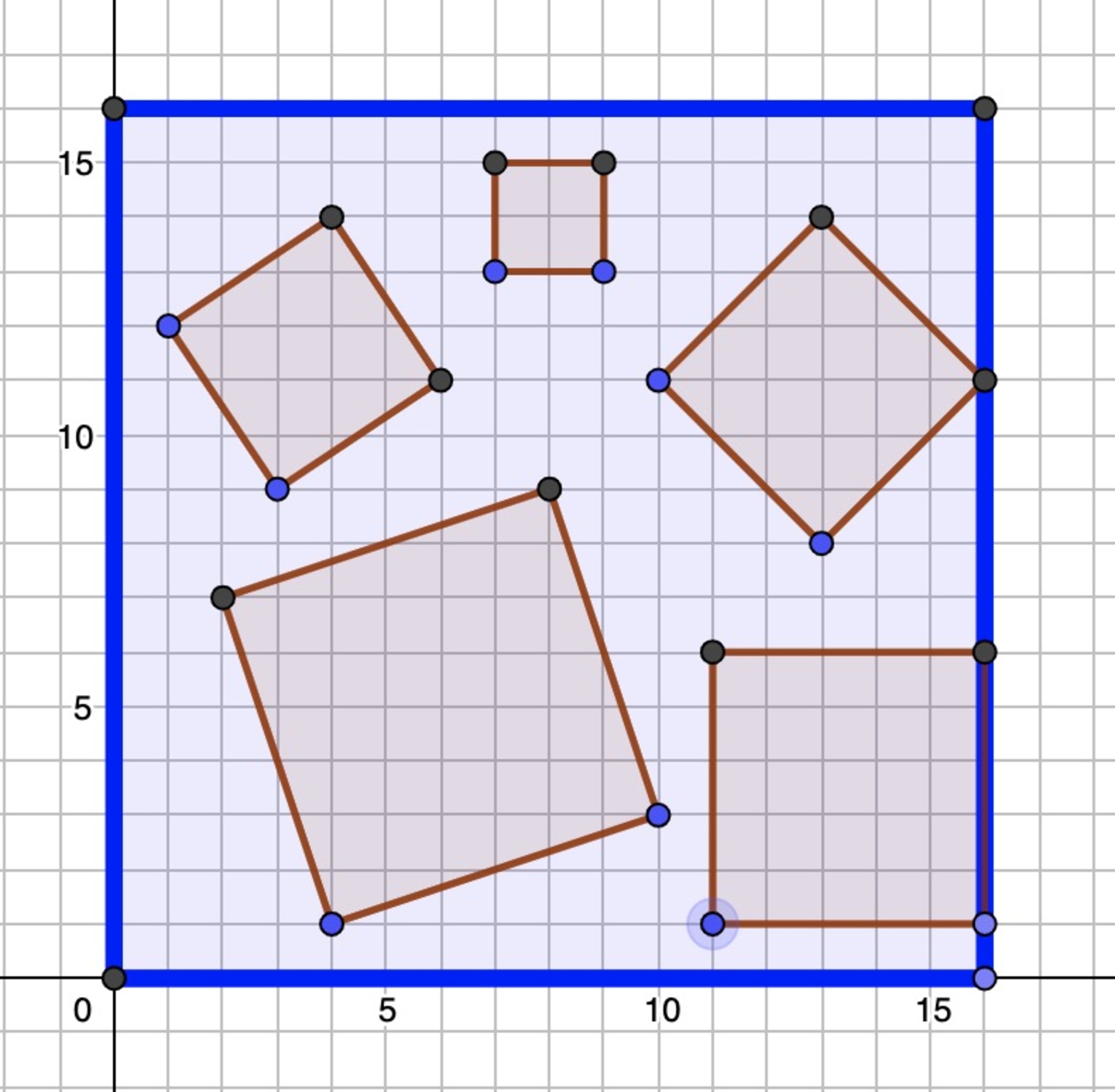
The answer is 6936.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Say the total number of squares we can draw on an n × n grid is f ( n ) .
Start drawing a square from a point on the grid A ( p , q ) . Draw the next vertex at B ( p + u , q + v ) . This defines the remaining vertices; the full set is A ( p , q ) B ( p + u , q + v ) C ( p + u − v , q + v − u ) D ( p − v , q − u )
To make sure it fits on the grid, we need 0 ≤ p − v , 0 ≤ q − u , p + u ≤ n q + v ≤ n
This gives n + 1 − u − v possible values of p and the same for q . For a fixed pair ( u , v ) satisfying u + v 0 ≤ n , this means there are a total of ( n + 1 − u − v ) 2 possible starting points ( p , q ) so that all vertices are on the grid.
In order to avoid double-counting we just need to insist that u ≥ 0 and v ≥ 1 (this avoids counting squares with sides on the gridlines twice).
This gives the formula f ( n ) = u = 0 ∑ n − 1 v = 1 ∑ n − u ( n + 1 − u − v ) 2
...which looks pretty horrendous, but after doing the paperwork** we get the surprisingly neat f ( n ) = 1 2 1 n ( n + 1 ) 2 ( n + 2 )
In particular, f ( 1 6 ) = 6 9 3 6 .
**There are various ways to work out the sum, such as:
Expand, and use the formulas for ∑ k and ∑ k 2 repeatedly
Use Wolfram|Alpha to help
Recognise it will be a polynomial in n , calculate some values and use a difference table to work out coefficients
I suspect there's a clever way to use symmetry here too, but perhaps that's a bonus question?