How many triangles?
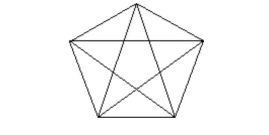 How many triangles are in a fully connected pentagon with all its diagonals?
How many triangles are in a fully connected pentagon with all its diagonals?
The answer is 35.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
That's a clear way of counting to ensure we got everything.
Log in to reply
Can we use the compliment rule here? Eg. Total triangles using all points - those triangles which aren't able to form due to collinearity = 10C3 - 5(4C3) but something is wrong answer isn't coming. :/ help
Log in to reply
There are many more sets of 3 points which do not yield a triangle (with lines given by that in the diagram). For example, take any 2 points on the inner pentagon, and 1 point on the outer pentagon (which also includes the case of 3 collinear points like you mentioned).
Yeah, I did the same. It should be a combinatorics problem instead of geometry problem.
Firstly there are 10 small outer triangles around the edge of the pentagon.
Secondly there are 5 large triangles given by any 2 adjacent points on the outer pentagon and the point on the opposite side.
Inside each of these 5 triangles there are 4 more triangles giving us the total of: 1 0 + 5 + ( 5 × 4 ) = 3 5
5 main triangles in the pentagon , each gives 7 so 5 * 7 gives 35
would you please tell me how it is???
What do you mean by "5 main triangles, each gives 7"?
There is double-counting in your answer. Plus each main triangle has 9 triangles!! You made 2 mistakes and got the correct answer!!
How I counted: First forget the star and notice that the top triangle has 6 triangles are there are 5 of these so 6*5=30. Now looking at the star you see one more triangle which there are five of and so we can conclude 30+5=35
With each side of pentagon we are getting 4 triangles. So for 5 sides we r getting 5*4= 20 triangles. Taking 2 adjacent sides we are getting 5C2 =10 triangles. Lastly, we are getting 5 triangles from each vertices. Total no of triangles= 20+10+5=35
how do you get 4 triangles on each side of pentagon please make it clear
on each vertex there are 7 triangles :. there are 7times5=35
Can you explain what you mean by "on each vertex there are 7 triangles"? Also, won't this result in a lot of double counting?
Log in to reply
SIR is there any general formula for these type of questions
Log in to reply
Yes, there is a general formula for the generalization of this formula. However, instead of just memorizing the formula, you should seek to understand how one can perform such a counting, which would allow you to derive the answer for other cases.
As for "these types of questions", no not necessarily. Sometimes you need to do a case by case analysis.
Single triangle based are 10 ( at each vertex ), double triangle based are 10 ( at each vertex ) , triple triangle based are 5 ( at each vertex ) center pentagon+2 triangle based are 5 center pentagon+3 triangle based are 5
from each base of pentagon there are 3 triangles and 5 are inside it
First, any three points of the outer pentagon will give us a triangle ( 5C3); Next, we consider triangle that have 2 points outside and 1 point inside. With each point inside, there is one point outside that is not connected, and 2 pairs of point that in a line, leaving 4C2 - 2 = 4 options; and there are 5 points inside (5x4) Third, there are only 5 triangles with 2 points inside and 1 point outside, since 2 points inside must be next to together to be connected, and each pair has only 1 point outside that make them a triangle (5) There is no 3 points inside that all connected together. Hence, the answer is 5C3 + 5x4 + 5 = 35