How many triangles?
Probability
Level
2
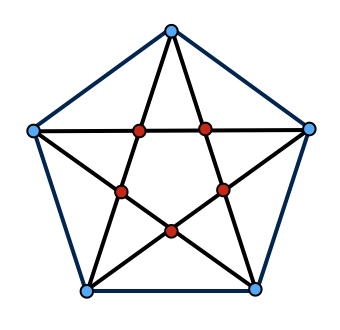How many triangles are in the figure above?
The answer is 35.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We can break up the cases in terms of what kinds of vertices the triangle has.
(1) All blue vertices.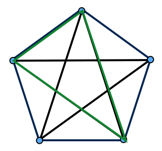
There is 1 triangle for each set of 3 of the blue vertices, so there are ( 3 5 ) = 1 0 of these type.
(2) Two adjacent blue vertices, one red vertex.
For each pair of adjacent blue vertices, there are 3 such triangles (see below). Thus, there are 5 ⋅ 3 = 1 5 triangles of these type.
(3) Two non-adjacent blue vertices, one red vertex.
For each pair of non-adjacent blue vertices, there is 1 such triangle (see below). Thus, there are 5 ⋅ 1 = 5 triangles of these type.
(4) One blue vertex, two red vertices.
For each blue vertex, there is 1 such triangle (see below). Thus, there are 5 ⋅ 1 = 5 triangles of these type.
(5) All red vertices.
No such triangles exist!
Thus, the total number of triangles is 1 0 + 1 5 + 5 + 5 = 3 5 triangles.