This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.

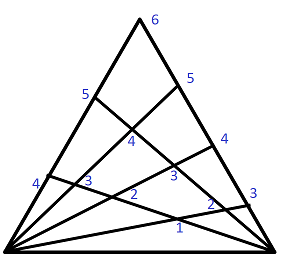
First note that any triangle obtained from this figure must
(i) be formed using 3 non-parallel lines, either 2 blue lines and 1 red line, OR 2 red lines and 1 blue line;
(ii) contain either the vertex A or the vertex B .
Let's consider those triangles containing the vertex A . The number of triangles is ( 2 5 ) × ( 1 3 ) = 3 0 . Then consider those triangles containing NO vertex A but vertex B , there are ( 2 3 ) × ( 1 4 ) = 1 2 such triangles. Hence there are a total of 4 2 triangles.
A video for the solution.