How many ways can it reach?

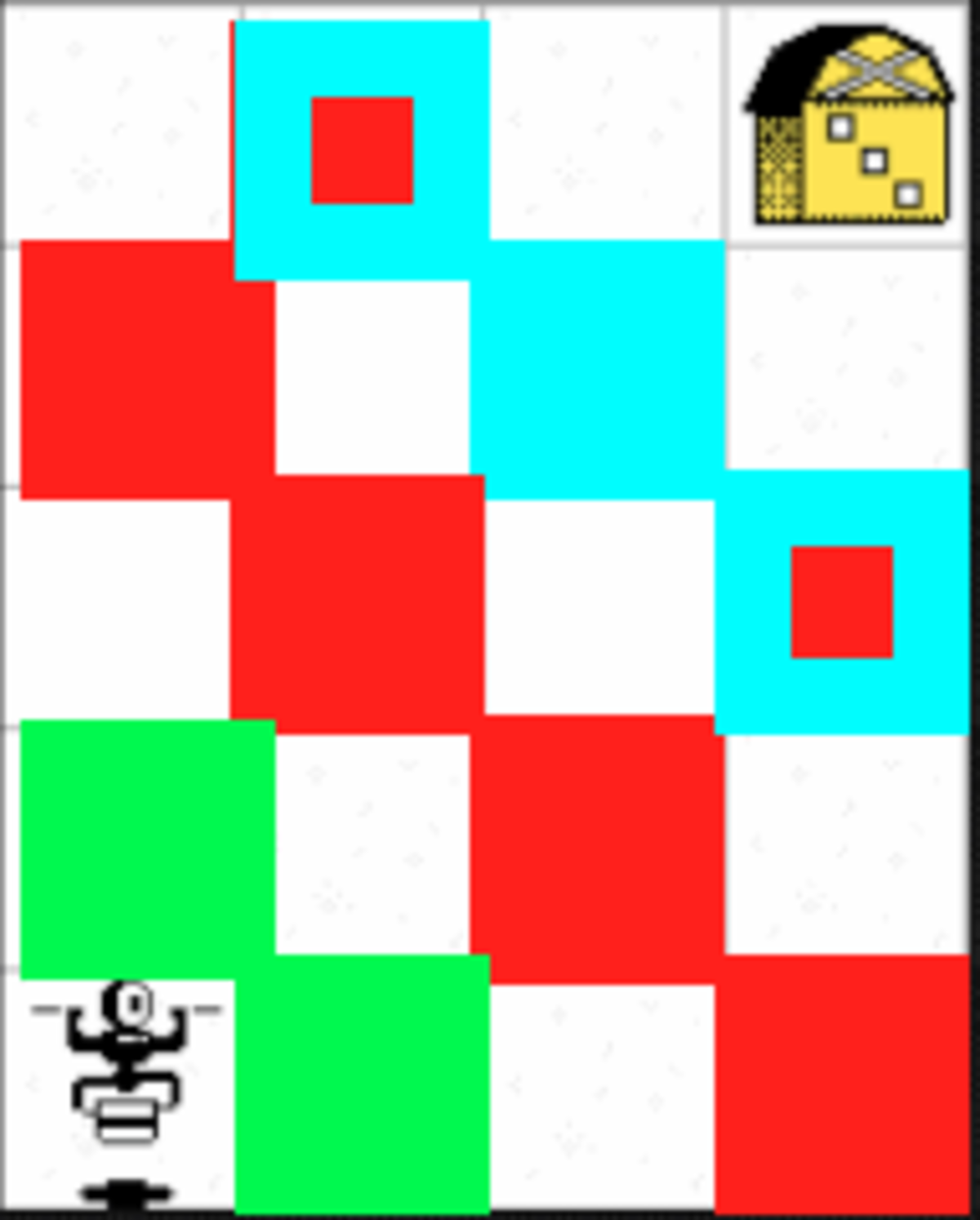What this is showing: the blue are two steps away from the barn the red are all two steps away from the blue the green are two steps away rom the red the red and blue are both two away from the barn and the blue you may notice that the green are one away from The Eye Of Amazoo but you have to get to the green (10-1=9). Then you use two more to get to the red(9-2=7) then the blue(7-2=5). since you need to burn off some steps, you can do 2 and not move(5-2=3). Now you cannot reach two from three by minus two, so it is impossible to reach the barn in 10 steps, or for that matter, any even amount of steps. If you have questions, please comment.

In an odd step we can go only to the black, and in an even, only to the white squares

In the 4 by 5 grid, we imagine a board where the amazoo bot is in a black squared box and the barn is in a light squared box

If we go one move, we are in a white box, if 2 then a black box, so even moves (like 10) can only land in a black square, and since the barn is in a light square(odd) it is imposible to go to the barn with 10 moves

Let:

$U$ number of Upward Moves $\quad$ $D$ number of Downward Moves $\quad$ $L$ number of Left Moves $\quad$ $R$ number of Right Moves

$\quad$

$\displaystyle U - D = 4$ ...Eq1

$\displaystyle R- L = 3$ ...Eq2

$\displaystyle U + D + L + R = 10$ ...Eq3

By Eq1:

$\displaystyle D = U -4$ ...Eq1'

By Eq2:

$\displaystyle L = R -3$ ...Eq2'

Substitute Eq1' & Eq2' $\to$ Eq3:

$\displaystyle 2U + 2R = 17$ ...Eq4

Since we require solutions for $R$ and $U$ to be in the positive integers, no solution exist because the LHS is always even and the RHS is odd.

For the robot to reach the barn with the least number of steps it has to travel 3 steps to the right and 4 steps upwards (overall 7 steps). Any moves that are down or left displace the robot from a shortest path.

If the robot has to reach the barn with 10 steps it must take extra steps, particularly in leftward and downward directions. Whenever the robot goes left or down, it has to travel right or up respectively to compensate its displacement from the shortest path, which was 7 steps. These extra movements come in pairs so if the robot goes left once than it also has to travel to the right once at some point. Since the original number of steps without extra steps was 7, which is an odd number, any kind of extra movements will add 2 more steps, making it impossible to reach the goal of 10 steps, because it is an even number.