How many ways can you color this?
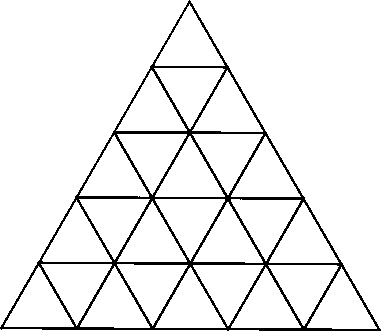
This is a "5-Check" triangle and is being colored using Red and Cyan.In a way such that three small triangles are Red and rest are Cyan.
Two Patterns are called "clones" if one can be rotated one-third ways to get another
So the three patterns below are "clones".
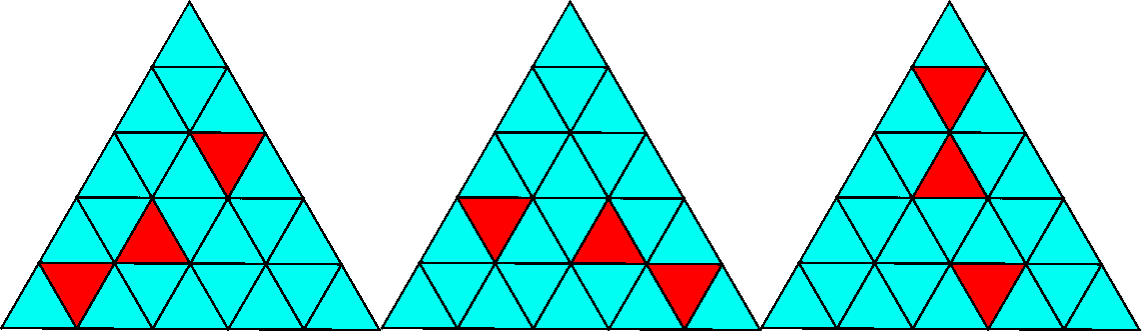
In " -Check" triangle,a set of pattern is called "okay.." if there are no two patterns which are clones to each other.
For what can be the maximum number of elements in it's corresponding "okay.." set?
PS:Sorry for the bad image quality.
The answer is 6152.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
There are 7 2 = 4 9 smaller triangles in a 7 -check triangle, and there are 4 9 C 3 ways to choose 3 smaller triangles out of the total 4 9 .
However, all of these will have 3 duplicates through rotational symmetry except for 1 6 C 1 of them, the number of ways to choose 1 triangle out of the 1 6 triangles that make up a third symmetrical section of the whole.
So the maximum number of elements in a corresponding "okay" set will be 3 4 9 C 3 − 1 6 C 1 + 1 6 C 1 = 3 1 8 4 2 4 − 1 6 + 1 6 = 6 5 2 .