How Much Area is Left 2

Algebra Level 2

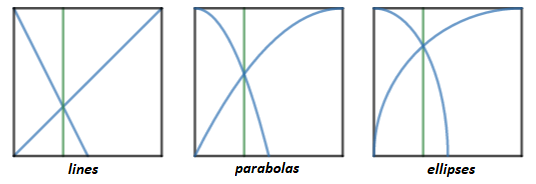
Let $x_{\text{line}}$ be the $x$ -coordinate of the intersection of the line through $(1, 1)$ and $(0, 0)$ and the line through $(0, 1)$ and $(\frac{1}{k}, 0)$ for $k \geq 1$ and $0 \leq x_{\text{line}} \leq 1$ .

Let $x_{\text{parabola}}$ be the $x$ -coordinate of the intersection of the parabola with vertex $(1, 1)$ through $(0, 0)$ and the parabola with vertex $(0, 1)$ , and through $(\frac{1}{k}, 0)$ for $k \geq 1$ and $0 \leq x_{\text{parabola}} \leq 1$ .

Let $x_{\text{ellipse}}$ be the $x$ -coordinate of the intersection of the ellipse with vertex $(1, 1)$ , co-vertex $(0, 0)$ , and center $(1, 0)$ and the ellipse with vertex $(0, 1)$ , co-vertex $(\frac{1}{k}, 0)$ , and center $(0, 0)$ for $k \geq 1$ and $0 \leq x_{\text{ellipse}} \leq 1$ .

Out of $x_{\text{line}}$ , $x_{\text{parabola}}$ , and $x_{\text{ellipse}}$ , which one has the greatest value?

Inspiration

x_{\text{line}}

x_{\text{ellipse}}

they all have the same value

x_{\text{parabola}}

it depends on

k

1 solution

David Vreken
May 2, 2019

In all three cases, if $f(x)$ is the first function through $(1, 1)$ and $(0, 0)$ and $g(x)$ is the second function through $(0, 1)$ and $(\frac{1}{k}, 0)$ , then $g(x)$ is $f(x)$ shifted $1$ unit to the left, reflected in the $y$ -axis, and stretched by a factor of $\frac{1}{k}$ , so that $g(x) = f(-kx + 1)$ . The intersection of $f(x)$ and $g(x)$ therefore occurs when $x = -kx + 1$ , which solves to $x = \frac{1}{k + 1}$ . Therefore, $x_{\text{line}} = x_{\text{parabola}} = x_{\text{ellipse}} = \frac{1}{k + 1}$ , so they all have the same value .

The image below shows that $x_{\text{line}} = x_{\text{parabola}} = x_{\text{ellipse}} = \frac{1}{3}$ for $k = 2$ :

I got close! Wish I could give more than one "brilliant" for this solution, it's very elegant.

Chris Lewis - 2 years, 1 month ago

Thank you!

David Vreken - 2 years, 1 month ago

How Much Area is Left 2

1 solution

0 pending reports