How Much Can We Squeeze In?
Geometry
Level
3
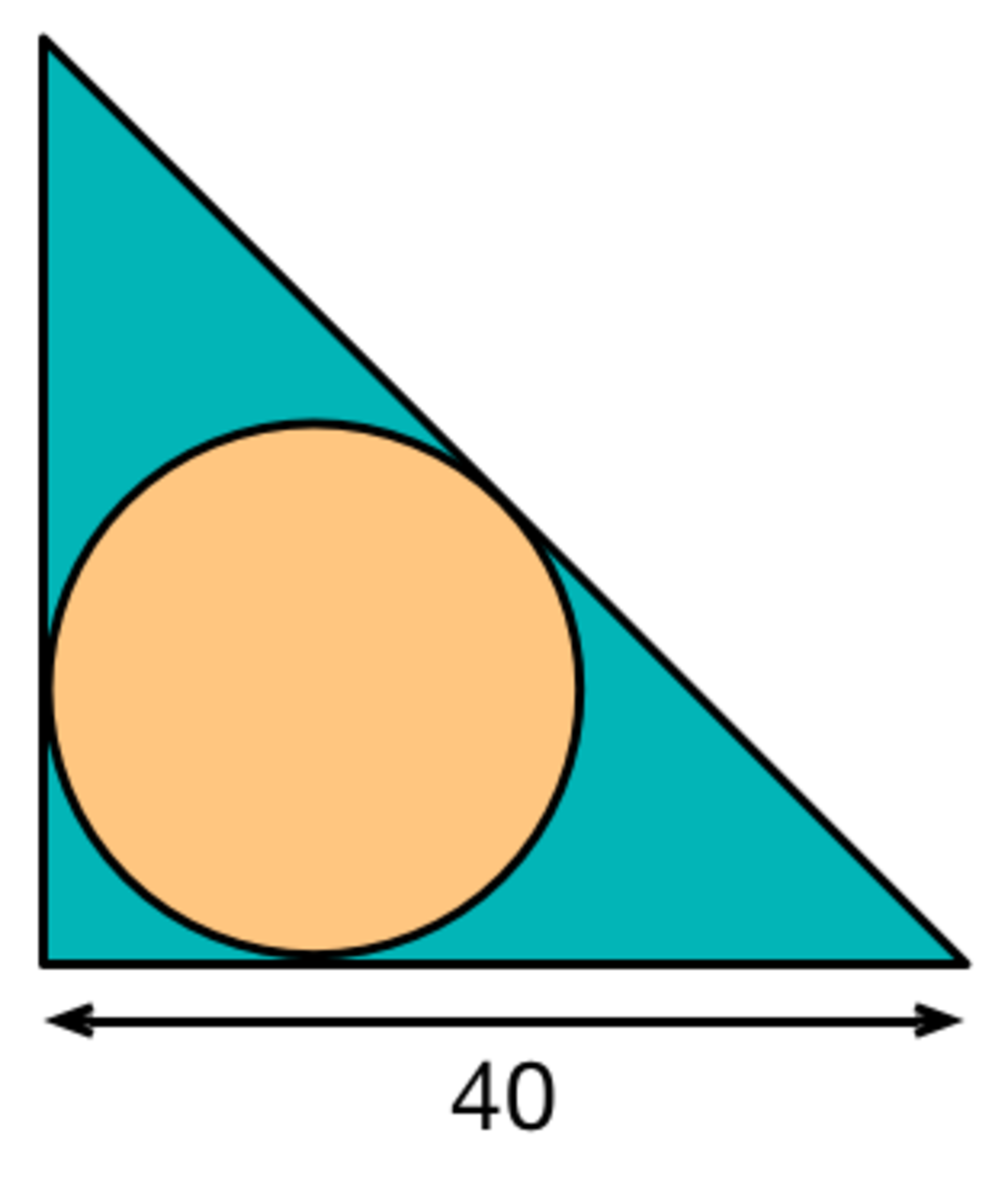
What is the largest integer diameter of a circle that we can fit into an isosceles right triangle with length 40?
20
21
22
23
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Remember that the radius of the largest inscribable circle in a triangle is equal to the area of the triangle divided by the semi-perimeter. That is 2 4 0 × 4 0 divided by 2 4 0 + 4 0 + 4 0 2 = 4 0 + 2 0 2 8 0 0 = approx. 11.716. But this is the diameter so we have to multiply it by 2 which yields 23.431 which we round down to 2 3 .