How Much Does It Slide?

Classical Mechanics Level 2

A bullet of mass 0.02 kg travelling horizontally with velocity 250 m/s strikes a block of wood of mass 0.23 kg which rests on a rough horizontal surface. After the impact, the block and bullet move together and come to rest after travelling a distance of 40 m. What is the coefficient of sliding friction of the rough surface ????? (g = 9.8 m/s )

0.30 0.51 0.75 0.61

2 solutions

Kãŕtįk Cämérøñ
May 22, 2015

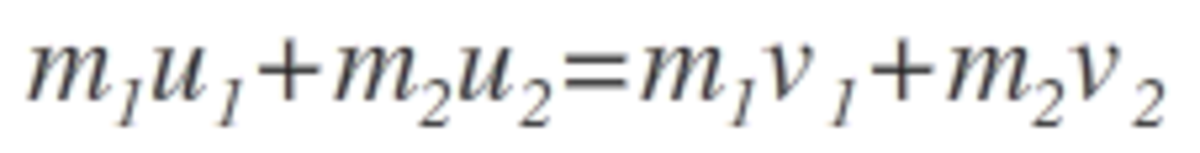
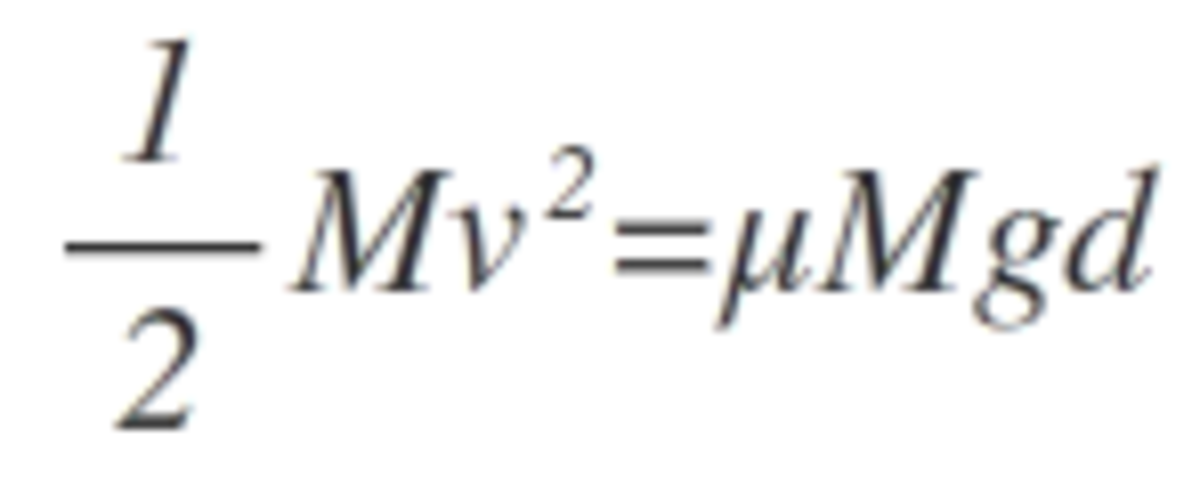
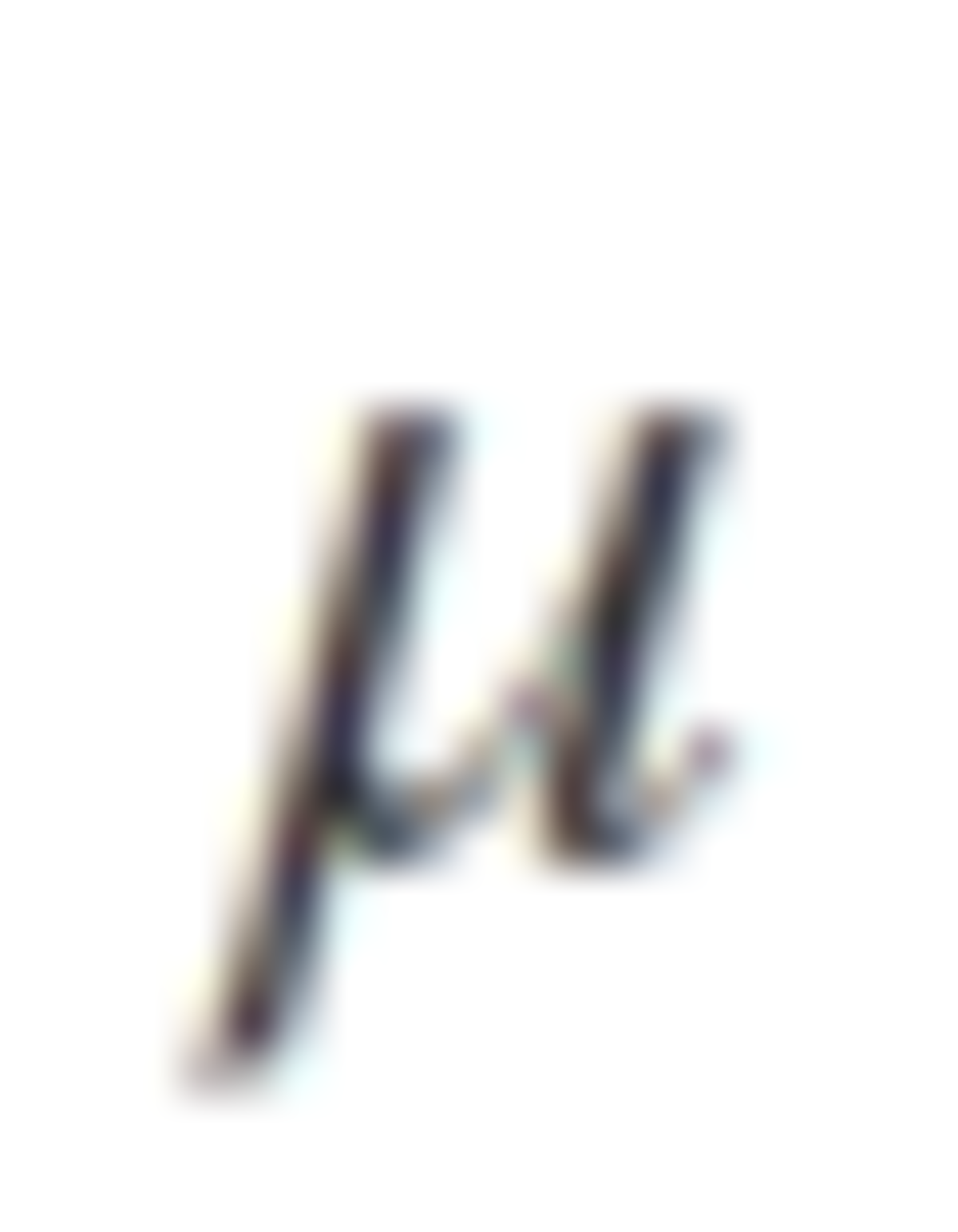
M1V1= M2V2 M2 = 0.23+0.02=0.25 we will thereby get, V2 = 20m/s coeffecient sliding friction = force / normal reaction = m.a/m.g = a/g v^2 - u^2 = 2.a.s (we know v=0 , object came to rest) -400 = 2.40.a a = -50m/s coefficient of sliding friction= -50/9.8= 5.1 '-' only denotes direction here

Gagan Raj
Mar 1, 2015

After the impact the bullet and the block move together and come to rest after covering a distance of 40m.

By Law Of Conversation Of Momentum ,

$0.02\times250 + 0.23\times0$ $=$ $0.02v + 0.23v$

$5+0$ $=$ $0.25v$

$v = 500/25 = 20 m/s$

Now , By Law Of Conversation Of Energy ,

$0.5\times0.25\times400$ $=$ $\times0.25\times9.8\times40$

$=$ $0.51$ .

How Much Does It Slide?

2 solutions

0 pending reports