How much does the CM go up?
Consider a homogeneous cylinder of radius
r
=
1
and height
h
=
2
. Cut out a hemisphere of radius 1 from the bottom and place it on top.
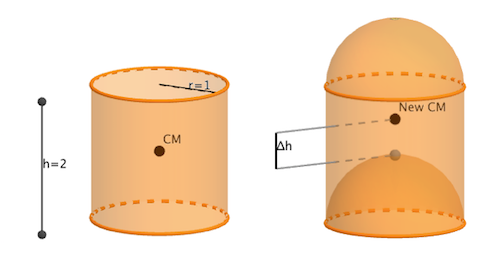
The new body's center of mass will lie at a distance Δ h = b a where a and b are coprime positive integers. Find a + b .
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Nice simple solution!
Consider the new body as formed by three pieces: the original cylinder, of m c = π r 2 h ρ = 2 π ρ (where ρ is the density) , the top hemisphere, of mass m t = 3 2 π r 3 ρ = 3 2 π ρ , and a bottom hemisphere of negative mass m b = − 3 2 π ρ . The superposition of this negative mass and the cylinder creates the hollow base.
To focus on the physics of the problem, I leave it up to you to prove that the CM of a hemisphere of radius r lies at a height h = 8 3 r above the base center.
Referencing all positions to the cylinder's CM, the CM's heights of the top and bottom hemispheres are h t = 1 + 8 3 = 8 1 1 and h b = − 1 + 8 3 = − 8 5 respectively.
We now calculate the CM of the resulting system:
Δ h = m c + m t + m b m c ⋅ h c + m t ⋅ h t + m b ⋅ h b = 2 π ρ 2 π ρ ⋅ 0 + 3 2 π ρ ⋅ 8 1 1 + ( − 3 2 π ρ ) ⋅ ( − 8 5 ) = 3 2 Therefore, a = 2 , b = 3 and a + b = 5 .
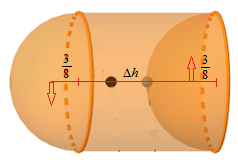
We can find that the center of mass of hemisphere is 8 3 of its radius from its base (see note). Then taking moment about the old center of mass, considering empty space as negative mass and let the density of the solid be ρ , we have:
2 π ρ Δ h ⟹ Δ h = 3 2 π ρ ( 1 + 8 3 ) + 3 2 π ρ ( 1 − 8 3 ) = 3 1 ( 8 1 1 ) + 3 1 ( 8 5 ) = 3 2
Therefore, a + b = 2 + 3 = 5 .
Note: Let the center of the hemisphere of radius R and density ρ be the origin ( 0 , 0 , 0 ) and its base normal to the x -axis. Then its center of mass from the center is given by:
h = 3 2 π ρ R 3 ∫ 0 R x y 2 d x = 2 R 3 3 ∫ 0 1 x ( R 2 − x 2 ) d x = 2 R 3 3 [ 2 R 2 x 2 − 4 x 4 ] 0 R = 8 3 R
It is convenient to compute the new center of mass in cylindrical coordinates: 2 π 1 ∫ 0 2 π ∫ 0 1 ∫ 1 − r 2 2 + 1 − r 2 z r d z d r d θ = 3 5 . The shift is Δ h = 3 2 and the answer is 5 .
@Otto Bretscher I am not able to understand your technique. Can you bit explain. Please sir??
V h e m i s p h e r e = 6 4 π r 3 = 3 2 π
V c y l i n d e r = π r 2 h = 2 π
This means that
V c y l i n d e r V h e m i s p h e r e = 2 π 3 2 π = 3 1
of the cylinder has been moved.
Since the hemisphere was moved by 2 units, the center of mass has gone up by 2 ⋅ 3 1 = 3 2 units, so the answer is 2 + 3 = 5 .
I don't know the conditions for this method to work, but I think the body has to have rotational symmetry.