How Much is Green?

Geometry Level 1

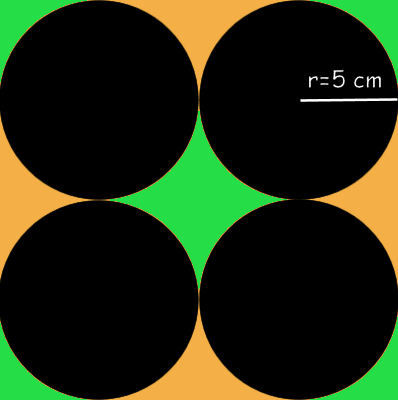4 identical black circles of radii 5 cm are drawn on a square background with sides of 20 cm. The circles touch but do not overlap each other and the edge of the background.

What is the total area of the green sections? (to 2 decimal places)


The answer is 42.92.

Guiseppi Butel by Guiseppi Butel , 90, Canada

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

5 solutions

Max Sánchez
Jun 7, 2014

If we divide the square into 4 equal squares, we will get that each circle is in one square, that has 10 cm of side Then, the green area will be [(Area of square)-(Area of Circle)]/2=(100-25pi)/2 Then, that in 4 squares: 4(100 - 25pi)/2=2(100-25pi)=200-50pi=42.92 square cm

1 Helpful 0 Interesting 0 Brilliant 0 Confused

MY ANSWER IS TOO CLOSED TO THE CORRECT ANSWER

mj villamon - 6 years, 11 months ago
Guiseppi Butel
Jun 6, 2014

Area of the square is 20 x 20 = 400 cm^2

Area of the 4 circles = 4 * pi * 5^2 = 314.1542654 cm^2

Area of the greens = (Area of square - Area of circles)/2 = 42.92 cm^2

1 Helpful 0 Interesting 0 Brilliant 0 Confused

No this is the area of greens + oranges

Samarth Chandrawat - 7 years ago

Log in to reply

I divided this by 2.

Perhaps you didn't notice the / sign.

Guiseppi Butel - 7 years ago

i was just near

shashwat sangle - 6 years, 11 months ago
Rifath Rahman
Jun 30, 2014

IF WE TAKE 4 SQUARES WITH SIDES OF 5 INCLUDING THE CIRCLE AND GREEN AREA THEN THE AREA OF THE GREEN AREA IS (25-(25 pi)/4)=5.365,AS THERE ARE 4 OF THOSE THE AREA BECOMES 4 5.365=21.46,NOW IN MIDDLE WE IMAGINE A SQUARE HAVING THE SIDE OF 10 THEN THE GREEN AREA IS (AREA OF SQUARE-4 AREA OF THE CIRCLES/4)=(AREA OF THE SQUARE-AREA OF A CIRCLE)=100-25 pi=21.46 SO THE WHOLE GREEN AREA IS 21.46+21.46=42.92

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Sachin Sp
Jun 21, 2014

Area of the square is 20 x 20 = 400cm^2, Area of the 4 circles =78.5714 x 4 =314.285, Area of the square - Area of the 4 circles = 86, 86/2 = 43

0 Helpful 0 Interesting 0 Brilliant 0 Confused

The answer is to be given in cm^2, and this should be specified in the statement of the problem ;-)

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...