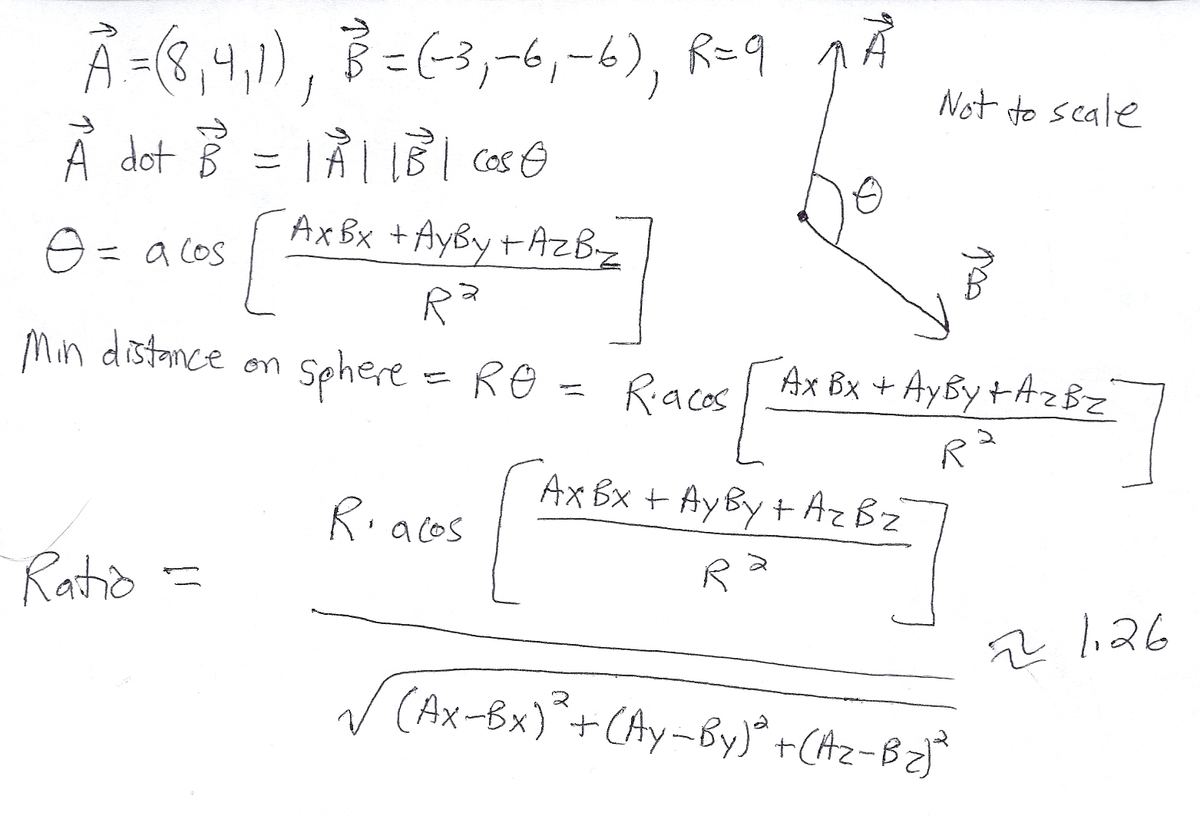
How Much Shorter is the Straight Line?
Consider a sphere of radius R = 9 centered on the origin ( x , y , z ) = ( 0 , 0 , 0 ) . Find the minimum path length from ( 8 , 4 , 1 ) to ( − 3 , − 6 , − 6 ) , subject to the constraint that the path must not leave the sphere's surface.
Enter your answer as the ratio of this distance to the straight-line distance between the two points.
The answer is 1.26.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
S t r a i g h t − l i n e d i s t a n c e = [ 8 − ( − 3 ) ] 2 + [ 4 − ( − 6 ) ] 2 + [ 1 − ( − 6 ) ] 2 = 2 7 0 This line forms an isosceles triangle at the center with the two radius, and say vertex angle X. X = ( 2 ∗ S i n − 1 2 ∗ 9 2 7 0 ) c . S o t h e a r c d i s t a n c e = ( 2 ∗ S i n − 1 2 ∗ 9 2 7 0 ) c ∗ 9 . ∴ r e q u i r e d r a t i o = 2 7 0 2 ∗ S i n − 1 2 ∗ 9 2 7 0 c ∗ 9 . = 1 . 2 6 0 0
Take a circle of radius 9 . Now let a given chord of thus circle subtend angle θ at centre.
The minor arc represnts the smallest path on sphere and path along chord is straigh line distance.
Thus 1 8 s i n ( θ / 2 ) = 2 7 0 .
And arc length = 9 × θ
Key to answer : Visualisation in 3-D + 2-D .