How much should this farmer produce ?.

• Potato: The farmer can produce $1 \text{ kg}$ of potato with $50 \text{ m}^2$ of land or $\frac 1{50} = 0.02 \text{ kg/m}^2$ which gives a profit of $p_p = 0.02 \times 2 = \$0.04/\text{m}^2$ of land.
• Tomato: The farmer can produce $1 \text{ kg}$ of tomato with $20 \text{ m}^2$ of land or $\frac 1{20} = 0.05 \text{ kg/m}^2$ which gives a profit of $p_t = 0.05 \times 1 = \$0.05/\text{m}^2$ of land.

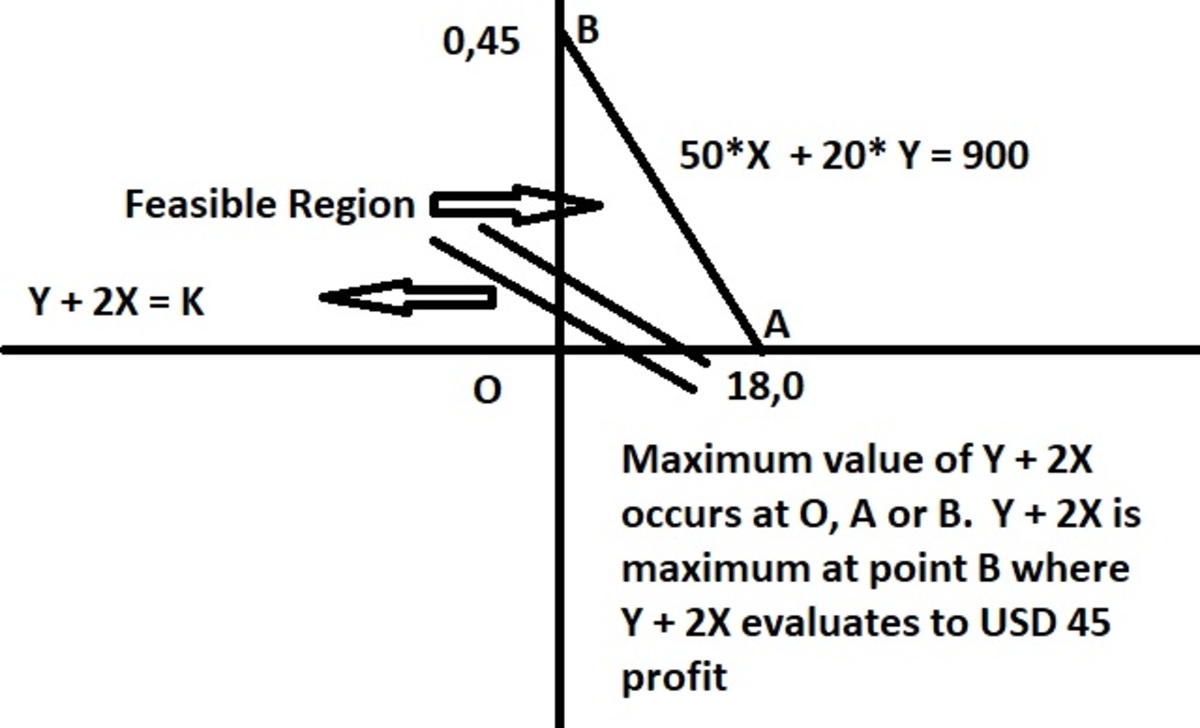
Since the farmer gets higher profit planting tomato per $\text{m}^2$ of land, he obviously plants all land available with tomato. That is to produce $1000 \times 90 \% \times 0.05 = 45 \text{ kg}$ of tomato and $\text{ 0 kg}$ of potato.

Let X be the kgs of Potatoes and Y be the kgs of tomatoes that the farmer has to produce.

The profit function can be written as Y + 2X. This is shown in the graph above as family of lines with Y + 2X = K.

The constraint on the production is the utilization of the cultivatable area. The total cultivatable area for producing Xkgs of Potatoes and Y kgs of tomatoes can be represented by the function 50* X + 20 * Y. Since the maximum possible cultivatable area is 900 sq metre. The constraint to farm production can be written as 50 * X + 20* Y <= 900.

This is shown in the graph above. The maximum value of Y + 2X occurs when Y = 45 with a maximum profit of USD 45. In other words to achieve maximum profit the farmer has to cultivate 45 kgs of tomatoes.

Linear Programming