How to bundle π and e in a single integral

There are a few ways to do this, but the fastest one is probably through complex analysis and residue theory:

Consider the integral: $\oint_C \frac{e^{iz}}{1+z^2}dz$ where $z=x+iy \in \mathbb{C}$ . C is defined as the (closed) semi-circle of radius $R$ on the upper plane of the complex plane.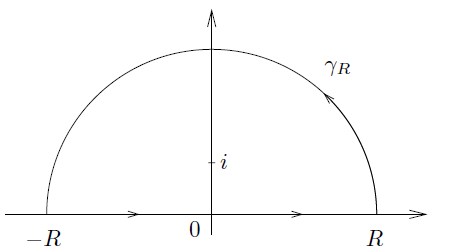

By the residue theorem, since $\forall R$ large enough, the pole of the integrand (namely $z = i$ ) is inside our contour, while the other ( $z = -i$ ) is not. Thus, we have:

$I = \oint_C \frac{e^{iz}}{1+z^2}dz = 2\pi i \left [ \frac{e^{iz}}{i+z} \right ] \Bigg|_{z=i} = \frac{\pi}{e}$

On the other hand, we can split our integral into two parts: integrate from $-R$ to $R$ (over the real-axis), then integrate over the semi-circle C'. In the later case, perform the change of variable $z = Re^{i\theta}$ and obtain:

$\int_{C'} \frac{e^{iz}}{1+z^2}dz = \int_0^\pi \frac{R e^{iR(\cos \theta +i \sin \theta)}}{e^{-i\theta}(1+R^2e^{2i\theta})} d \theta$

Now, it is not hard to see that the integrand goes to zero as $R \rightarrow \infty$ . In this limit, this integral thus vanishes and we are left with:

$\lim_{R \rightarrow \infty} \int_{-R}^R \frac{e^{ix}}{1+x^2} = \int_{-\infty}^{\infty} \frac{e^{ix}}{1+x^2} = \frac{\pi}{e}$ as required.