Can It Make A Triangle?
Two points are chosen randomly and uniformly along a stick of length 1 . The stick is cut at those points to form 3 pieces. What is the probability that these pieces can form a triangle?
The answer is 0.25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Wow, I should actually remember this kind of a solution! Very nice!
Imagine the rod on a number line so that one end is at x = 0 and the other at x = 1 . Now cutting the rod into 3 pieces involves making 2 cuts, call them x 1 and x 2 . By the triangle inequality, the 3 pieces resulting from the 2 cuts can form a triangle only if none of the pieces exceeds a length of 2 1 .
Now suppose the first cut x 1 lies on the interval [ 0 , 2 1 ] , (which will occur with probability 2 1 ). Then to ensure that no piece exceeds a length of 2 1 , the second cut would need to occur somewhere on the interval [ 2 1 , ( x 1 + 2 1 ) ] , which will occur with probability ( x 1 + 2 1 ) − 2 1 = x 1 . Now since the domain of x 1 is uniform over the interval [ 0 , 2 1 ] , the probability that the pieces can form a triangle will be
∫ 0 2 1 x 1 d x 1 = 8 1 .
By symmetry, the same result will be found if x 1 lies in the interval [ 2 1 , 1 ] , giving a final probability of 2 ∗ 8 1 = 4 1 = 0 . 2 5 .
any way we can use cosine rule or sine rule or any other properties of traingle to determine the answer
Log in to reply
I'm not sure if those rules would be much use here. Have a look at the link that Jake has provided for some alternative solution methods.
no other way to do it? @Brian Charlesworth
Log in to reply
The chosen answer is an amazing solution.
Jake's link does provide an excellent solution; I had to read it a few times to convince myself that it works, and now I appreciate its elegance.
In the link there is a further link to "these homework questions", in which the solution to question #5 outlines a geometric approach; no calculus required. Sometimes I find that calculus makes me less creative; I should try first to find solution methods without it, and only resort to it when absolutely necessary. :)
@Brian Charlesworth Sir , please help me out with your solution. When the cut x1 is made between 1/2 and 1 , how can a triangle form?
I think a simpler way than all others is to think that both the points lie on opposite side of the mid point of the line... This would imply that first point lying in the first half gjves probability 1/2 and same with other point which must be on the other side... Therefore probability of both points lying opposite sides of mid point of line is 1/2*1/2 =1/4
A graphical solution: Draw a suare diagram: on X axis is the first cut, on Y axis is the second cut. Hached area is where a triange is possible White are is where a triangle is possible
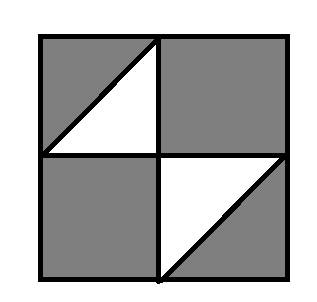 Answer: 0.25
Answer: 0.25
Say we cut the stick (which will here represent [ 0 , 1 ] ) into three pieces of length a , b , c , and assume that a is the largest.
a + b + c = 1 and we require a < b + c in order to form a triangle. Since b + c = 1 − a we have a < 1 − a so a < 2 1
Lets assume our first cut is at some point x in the first half of the stick ( [ 0 , 2 1 ] ) for simplicity (w.l.o.g.), and note that the section of the stick where we can safely make the second cut is precisely [ 2 1 , x + 2 1 ] , whose length is x . Since x varies from 0 to 2 1 and is distributed uniformly, its expected value is 2 1 = 0 . 2 5
Do you mean its expected value is midway between 0 and 1/2 = 1/2 x 1/2 = 0.25?
Let the stick be broken into pieces of length p , q , 1 − p − q . Then by the triangle inequality, we have:
p + q > 1 − p − q ⇒ q > 1 / 2 − p p + 1 − p − q > q ⇒ 1 / 2 > q q + 1 − p − q > p ⇒ 1 / 2 > p
which are all the possible orderings. Combining the first and second inequalities, 1 / 2 − p < q < 1 / 2 .
Without loss of generality, pick length p first, as the pieces are still the same length after swapping p and q . We can pick any value of p between 0 and 1 , which has probability 1 in the sample space. Then q is in the region above q = 1 / 2 − p and below q = 1 / 2 , which has a probability of 1 / 2 by graphing (event A ).
Then the remaining length 1 − p − q must be positive. Adding p to both sides, 1 / 2 < p + q < 1 / 2 + p , so − 1 / 2 > − p − q > − 1 / 2 + − p as the sign flips when we multiply by a negative number, and adding 1 to both sides, 1 / 2 > 1 − p − q > 1 / 2 − p or 1 / 2 − p < 1 − p − q < 1 / 2 .
And 1 − p − q must be above 1 / 2 − p but below 1 / 2 , which is exactly the same probability as earlier: 1 / 2 , (event B ).
The lengths of q and 1 − p − q are independent as P ( A ∣ B ) = P ( A ∣ B ′ ) and P ( B ∣ A ) = P ( B ∣ A ′ ) : they are all 1 / 2 1 / 2 = 1 as 1 − 2 1 = 2 1 . Hence we can multiply the probabilities to get 1 ⋅ 1 / 2 ⋅ 1 / 2 = 4 1 .
You can also solve it graphically quite easily!
Let the break points be x and y , and by symmetry assume that y ≥ x . Our sample space looks like: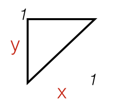
The lengths of the segments are x , y − x , 1 − y . The Triangle Inequality should hold for all 3 ordering of lengths:
x + ( y − x ) > 1 − y ⇒ y > 2 1
x + ( 1 − y ) > y − x ⇒ y < x + 2 1
( y − x ) + ( 1 − y ) > x ⇒ x < 2 1
Plotting this "good" region on our outcomes gives:
By Geometric Probability , the probability is thus area of all outcomes region area of good region = 1 / 2 1 / 8 = 4 1 = 0 . 2 5 .