How to measure g?
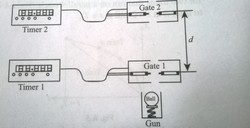 The figure shows a method for measuring the acceleration due to gravity. The ball is projected upwards by a "gun" . The ball passes the electronic" gates"1 and 2 as it rises and again as it falls . Each gate is connected to a separate timer . The first passage of the ball through each gate starts the corresponding timer ,and the second passage through the same gate stops the timer . The time intervals
and
are thus measured . The vertical distance between the two gates is "d". If d=5m and
=3 s and
=2 s , the find the measured value of acceleration due to gravity in S
I. Units.
The figure shows a method for measuring the acceleration due to gravity. The ball is projected upwards by a "gun" . The ball passes the electronic" gates"1 and 2 as it rises and again as it falls . Each gate is connected to a separate timer . The first passage of the ball through each gate starts the corresponding timer ,and the second passage through the same gate stops the timer . The time intervals
and
are thus measured . The vertical distance between the two gates is "d". If d=5m and
=3 s and
=2 s , the find the measured value of acceleration due to gravity in S
I. Units.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let's denote x as the distance from the peak of the ball to the gate. The initial velocity when the ball is at its peak is equal to 0 . The time taken from the peak to each of the respect gates should be be half the recorded values.
Using the equation d = v i t + 2 1 a t 2 , we make two equations by plugging in the values we know:
x = ( 0 m / s ) ( 2 s / 2 ) + 2 1 a ( 2 s / 2 ) 2
x + 5 m = ( 0 m / s ) ( 3 s / 2 ) + 2 1 a ( 3 s / 2 ) 2
Now, solving for a :
x = 2 1 a
2 1 a + 5 = 2 1 a 4 9
5 = 8 5 a
a = 8 m / s 2