How to: toss a ball into the bucket
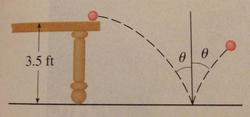 A ball rolls off a table with a speed of
. The table is
ft high.
A ball rolls off a table with a speed of
. The table is
ft high.
Suppose the ball rebounds from the floor at the same angle with which it hits the floor, but loses % of its speed due to energy absorbed by the ball on impact. Where does the ball strike the floor on the second bounce?
Enter the answer as the displacement of the ball in feet to the right of the table's edge.
Details and Assumptions :
- The table is perfectly horizontally flat (and so is the ground) - the picture is not drawn to scale.
- Round the answer to the nearest hundredth
The answer is 2.13.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.

Let time of first & second flight are t 1 & t 2
2 1 g t 1 2 = h ⇒ t 1 = 3 2 . 1 7 4 2 × 3 . 5 = 0 . 4 6 6 4 4 s e c R 1 = u t 1 = 2 × 0 . 4 6 6 4 4 = 0 . 9 3 2 8 8 f t
Let speed just before rebound is v.
The path of ball will be same if ball will be thrown towards table from that point with speed v so,
R 1 = 2 1 g v 2 s i n 2 θ ( m u l t i p l i e d b y 2 1 a s o n l y h a l f f l i g h t )
As it loses 20% speed,
R 2 = g ( 5 4 v ) 2 s i n 2 θ
R 2 = 2 5 1 6 g v 2 s i n 2 θ = 2 5 3 2 R 1 ⇒ A n s = R 1 + R 2 = ( 1 + 2 5 3 2 ) R 1 = 2 5 5 7 × 0 . 9 3 2 8 8 = 2 . 1 2 7 f t