How would you Handle The Ever-changing Logarithm? Part 1
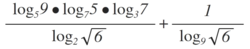 Imagine you are John Napier who arrived into this present future from the past, who was also credited for attributing to the success of deriving the concept of Logarithms and found answers to bizarre questions like
and introduced the letter L as 'Logarithm'.
Imagine you are John Napier who arrived into this present future from the past, who was also credited for attributing to the success of deriving the concept of Logarithms and found answers to bizarre questions like
and introduced the letter L as 'Logarithm'.
One Day, a mathematician approached him and was asking everyone on the street to evaluate this.....(above the passage).
Details : John was only given a pencil and an A4 piece of paper by the mathematician to attempt on the question and got the value of it quickly. The mathematician soon gave him a job and both continued to make great contributions in logarithms. (Do not use calculator to solve it)
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Apply lo g 1 0 = lo g on the expression, we have:
lo g 2 6 lo g 5 9 ˙ lo g 7 5 ˙ lo g 3 7 + lo g 2 6 1 = lo g 2 2 1 lo g 6 lo g 5 lo g 9 ˙ lo g 7 lo g 5 ˙ lo g 3 lo g 7 + lo g 9 2 1 lo g 6 1
= lo g 3 lo g 9 ˙ lo g 6 2 lo g 2 + lo g 6 2 lo g 9 = lo g 3 2 lo g 3 ˙ lo g 6 2 lo g 2 + lo g 6 4 lo g 3
= lo g 6 4 lo g 2 + 4 lo g 3 = lo g 6 4 ( lo g 2 + lo g 3 ) = lo g 6 4 lo g 6 = 4