How's That

According to Cosine Rule CosC= $\frac { ({ a }^{ 2 })+({ b }^{ 2 })-({ c }^{ 2 }) }{ 2ab }$

a,b,c are the sides of the triangle

As we know that the side c is the longest in the question

Now put the value in the given equation and you will get the answer as 120

Use vectors... let us assume triangle ABC with AB= a vector... AC = b vector... then |BC| = |b vector - a vector| = root ( a^2 + b^2 - 2 a b cos k) [ k is angle between them..]. but |BC| = root( a^2 + b^2 + ab)... therefore cos k = - 1/2 ............. k = 120 degrees

Note that $\sqrt{a^2+b^2+ab} > \sqrt{a^2+b^2}$ therefore $\theta > 90\deg$

Extending the triangle as shown we have:- $(a+x)^2+y^2=a^2+b^2+ab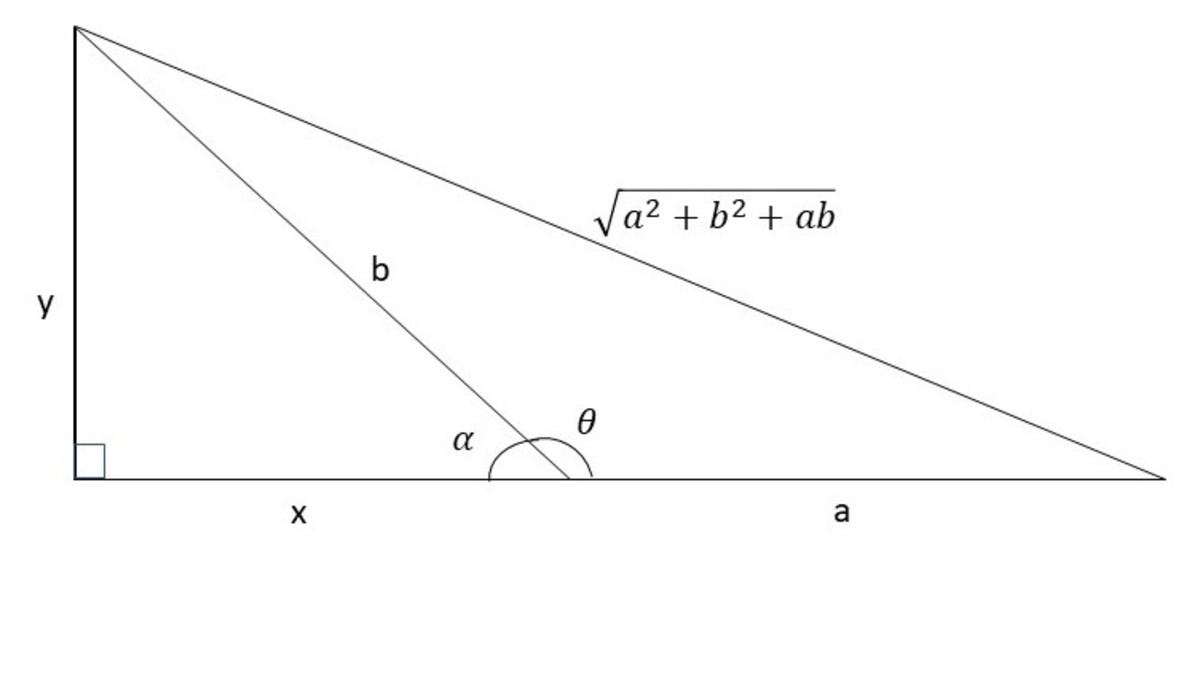$ Note that $y^2 = b^2-x^2$ so

$=>(a+x)^2 + b^2 - x^2 = a^2 + b^2 + ab$

$=> a^2+2ax+x^2+b^2-x^2=a^2+b^2+ab$

$=> 2ax = ab$

$=> x = \frac{b}{2}$

hence $\alpha = 60\deg => \theta = 180-60\deg$

$\boxed{\theta = 120\deg}$

*Bonus Question Solution : * $\quad$

First let's calculate Cosine of the angle 15.Those will be of use later in the solution.

$cos^2{15}=\frac{1+cos30}{2} \rightarrow cos^2{15} = \frac{1+\frac{\sqrt3}{2}}{2} \rightarrow \text{after simplifying}$

$\rightarrow cos15 = \frac{\sqrt{2+\sqrt3}}{2}$

$\quad$

Now let's calculate the Cosine of desired angle: $\quad$

$cos\alpha =\frac { ({ a }^{ 2 })+({ b }^{ 2 })-({ c }^{ 2 }) }{ 2ab } \rightarrow cos\alpha = \frac{-\sqrt2 -\sqrt6}{4} = -\frac{\sqrt{2+\sqrt3}}{2}$

Now note that:

$\quad$

$cos\alpha = -cos15 \rightarrow \text{Since the angles cannot exceed 180 degrees in a triangle}$

$\rightarrow \alpha = 165$

I need solution in detail please