Huckleberry Finn says hi
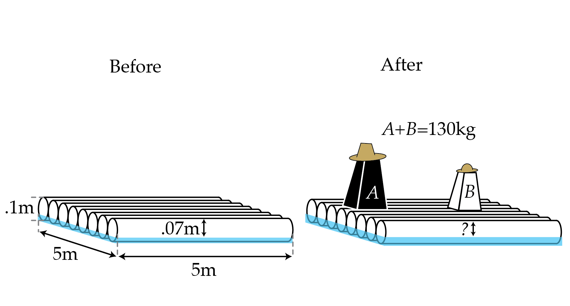
In Huckleberry Finn, a classic American novel by Mark Twain, much of the story takes place on a raft on the Mississippi river. Huckleberry's raft is a square 5 meters on a side with a vertical height of 0.1 m. If Huckleberry isn't on the raft it floats such that the top of the raft remains 0.07 m above the surface of the water. Huckleberry and his friend Jim, with a combined mass of 130 kg, climb on the raft. How far above the surface of the water in meters is the top of the raft after Huckleberry and Jim climb on?
Oh, and the Mississippi river is primarily fresh water...
Details and assumptions
- Treat the raft as just a rectangular prism/cuboid. You can ignore for the purposes of the problem that it's made of logs.
The answer is 0.0648.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
According to Archimedes' principle, the buoyant force on an object lowered into a fluid is F = ρ g V , where V is the volume of the displaced fluid. Note that since the raft is in equilibrium, the magnityde of this force must be equal to the rafts weight, m g , so F = ρ g V = m g , and ρ V = m We know the volume of the displaced fluid. Its area is 5 2 = 2 5 [ m 2 ] , and its depth is 0 . 1 − 0 . 0 7 = 0 . 0 3 [ m ] (note that the square brackets denote units). The density of water is very close to ρ = 1 0 3 [ k g / m 3 ] . So m = ρ V = 2 5 × 0 . 0 3 × 1 0 3 = 7 5 0 [ k g ]
Now, we add 1 3 0 [ k g ] , so the new mass is 7 5 0 + 1 3 0 = 8 8 0 [ k g ] . Let x be the new depth (the area is still 2 5 [ m 2 ] such that. V = 2 5 x . So, 8 8 0 = 2 5 x × 1 0 3 .
x = 2 5 × 1 0 3 8 8 0 = 0 . 0 3 5 2 [ m ] . This is the depth, so how far above the water the raft is, h , is just the total height minus x .
h = 0 . 1 − 0 . 0 3 5 2 = 0 . 0 6 4 8 [ m ]
Archimedes' Principle state that mg= \rho Vg where \rho is the density of water, V is the volume of the object immersed in water, m is the mass of the object and g is the gravitational acceleration.
The mass of the raft: m= \rho V, noted that the g has been cancel out.
m=1000kg m^{-3} \times (5m \times 5m \times 0.03m)
m=750kg
130kg(mass of two person) is then added and mass of raft and two person is 880kg.
Use the formula again, but with V=Area \times height of raft in water. 880kg=1000kg m^{-3} \times 25m^2 \times h
h=0.0352m
Therefore height of raft above the water surface is 0.1m-0.0352m=0.0648m
The mass of the raft is equal to the mass of the water displaced by the raft by itself, which is 5m * 5m * 0.03m * 1000kg/m^3 = 750kg. The total mass of the raft and the two boys is 880kg. Hence the volume of the water displaced by the raft with two boys is 880kg / 1000kg/m^3 = 0.88m^3.
Hence 0.88m^3 / 5m / 5m = 0.0352m of the raft is underwater. So the top of the raft is 0.1m - 0.0352m = 0.0648m above water.
initially 0.07m of raft is above the surface of water for extra weight,
equating weight and buoyant force
V
d
g = 130*g
25 * x * 1000 = 130,
where x is the height of raft to be immersed and density of water = 1000kg/m^3
x= 0.0052
so new height = 0.07- 0.0052 = 0.0648
The raft initially sinks 0.03 m into the water before it reaches equilibrium. Therefore we can find the mass of the raft using Newton's laws, the bouyant force, and the force of gravity:
F N e t = F b + F g = ρ V d g − m r a f t g = 0 ,
where ρ is the density of fresh water ( 1 0 0 0 k g / m 3 ) and V d is the displaced volume of water. We can therefore solve for
m r a f t = ρ V d = 1 0 0 0 × 0 . 0 3 × 5 × 5 = 7 5 0 k g .
Once Jim and Huck step on we can do another force balance,
ρ W d g − ( m r a f t + 1 3 0 ) g = 0 ,
and solve for W d , the displaced volume of the raft, as W d = 8 8 0 / 1 0 0 0 = 0 . 8 8 m 3 . Using W d = 2 5 h gives that the depth of the raft in the water is 0.0352 m which means the top is 0 . 1 − 0 . 0 3 5 2 = 0 . 0 6 4 8 m above the surface of the Mississippi.
Assuming a density of water 1000kg / m3 . The square raft will provide 250 kg per cm of immersion.
That figure come from flotation Area 25 m2 times 0.01m which amount to 250kg/cm Since the combined load is 130, the raft will sink 130/250 cm, therefore the free board will be reduced in such amount and we get 0.0648 m as new free board.
In its original state, the raft is in equilibrium with the weight of the raft balanced by the upthrust. m g = ρ V g m = ρ V . Given that the Mississippi river is primarily fresh water, \rho = 1000~kg/m^3/). We can thus work out the mass of the raft. \(m = 1000 \times 5 \times 5 \times (0.1-0.07) = 750~kg . When Huckleberry and Jim stand on the raft, a new equilibrium is established, and the upthrust exerted by the water is higher to support the additional downward force. Thus, letting x be the unknown distance, ( m + 1 3 0 ) = ρ ( V 1 ) 7 5 0 + 1 3 0 = 1 0 0 0 × 5 × 5 × ( 0 . 1 − x ) → x = 0 . 0 6 4 8 m .