HUH?! How to show the area given?
This question has troubled me for one day. I have searched all over the web but I can't find a proper slution!
UNDER THE CHAPTER OF DIFFERENTIATION
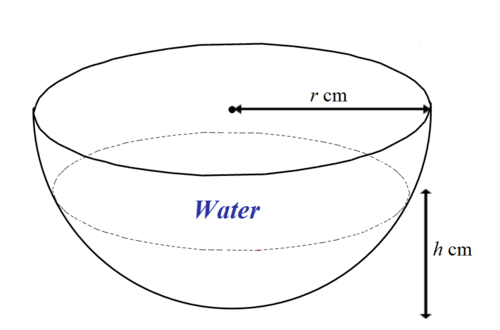
The diagram shows a hemispherical bowl with a radius of r cm. Water is poured into the bowl at a constant rate.
(a) Show that when the water level in the bowl is h cm, the surface area, A cm^2, of the water in the bowl is given by A = πh(2r - h). (b) If r = 5 and the rate of change in water level is 0.6 cm s^-1, find the rate of change in the surface area when h = 2.
* The answer provided is for question (b).
The answer is 11.3112.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
0 solutions
No explanations have been posted yet. Check back later!