Hunt for that Region!

Geometry Level 4

As shown, $AB=13, BC=15, AC=14$ in $\triangle ABC.$

Let $d(P,l)$ denote the perpendicular distance from point $P$ to line $l.$

Then find the area of the region enclosed by the traces of point $P$ satisfying $d(P,AB)>d(P,BC)>d(P,AC).$

Note: The desired region need not lie entirely within $\triangle ABC.$ For instance, for a point $P$ outside $\triangle ABC,$ the distance $d(P,AB)$ can be computed by dropping a perpendicular line from $P$ to the extended line of $AB.$

Food for thought: How would you define the area of the region to be finite?

You can try a similiar problem here .

This is part of the set Fun With Problem-Solving .

The answer is 60.

1 solution

Donglin Loo
Jun 3, 2018

Relevant wikis: Incenter , Incircles and Excircles

G is the incenter of $\Delta ABC$ and H is the excenter of $\Delta ABC$ . So, $d(G, AB) =d(G, BC) =d(G, AC)$ and $d(H, AB) =d(H, BC) =d(H, AC)$

The desired area is the sum of the area of the red triangle and the blue triangle.

$s=\cfrac{13+14+15}{2}=21$

By $\textbf{Heron's Formula}$ , Area of $\Delta ABC=\sqrt{21(21-13)(21-14)(21-15)}=84$

Let the radius of incircle of $\Delta ABC$ be $r$ .

Area of $\Delta ABC=r\cdot s$

$\therefore r=\cfrac{84}{21}=4$

$\because BD$ is the bisector of the interior angle $\angle ABC$

$\therefore \cfrac{AD}{CD}=\cfrac{AB}{CB}$

$\cfrac{AD}{DC}=\cfrac{13}{15}$

$\therefore DC=14\cdot\cfrac{15}{15+13}=\cfrac{15}{2}$

Area of $\Delta GDC$ (red triangle) $=\cfrac{1}{2}\cdot4\cdot\cfrac{15}{2}=15$

$\because CG$ is the bisector of the interior angle $\angle BCA$

$\therefore \cfrac{BG}{DG}=\cfrac{BC}{DC}$

$\cfrac{BG}{DG}=\cfrac{15}{\cfrac{15}{2}}=\cfrac{2}{1}$

$\because CH$ is the bisector of the exterior angle $\angle ACJ$

$\therefore \cfrac{BH}{DH}=\cfrac{BC}{DC}$

$\cfrac{BH}{DH}=\cfrac{15}{\cfrac{15}{2}}=\cfrac{2}{1}$

$\cfrac{BD}{DH}=\cfrac{1}{1}$

$BD=DH$

$\Delta GDC$ and $\Delta DHC$ share the common height

$\therefore \cfrac{Area of \Delta GDC}{Area of \Delta DHC}=\cfrac{GD}{DH}=\cfrac{GD}{BD}$

We have shown that $\cfrac{BG}{DG}=\cfrac{2}{1}$

$\therefore \cfrac{Area of \Delta GDC}{Area of \Delta DHC}=\cfrac{GD}{BD}=\cfrac{1}{1+2}=\cfrac{1}{3}$

$\Rightarrow \cfrac{15}{Area of \Delta DHC}=\cfrac{1}{3}$

Area of $\Delta DHC$ (blue triangle) $=15\cdot3=45$

Area of desired region $=15+45=60$

$\textbf{Food for Thought:}$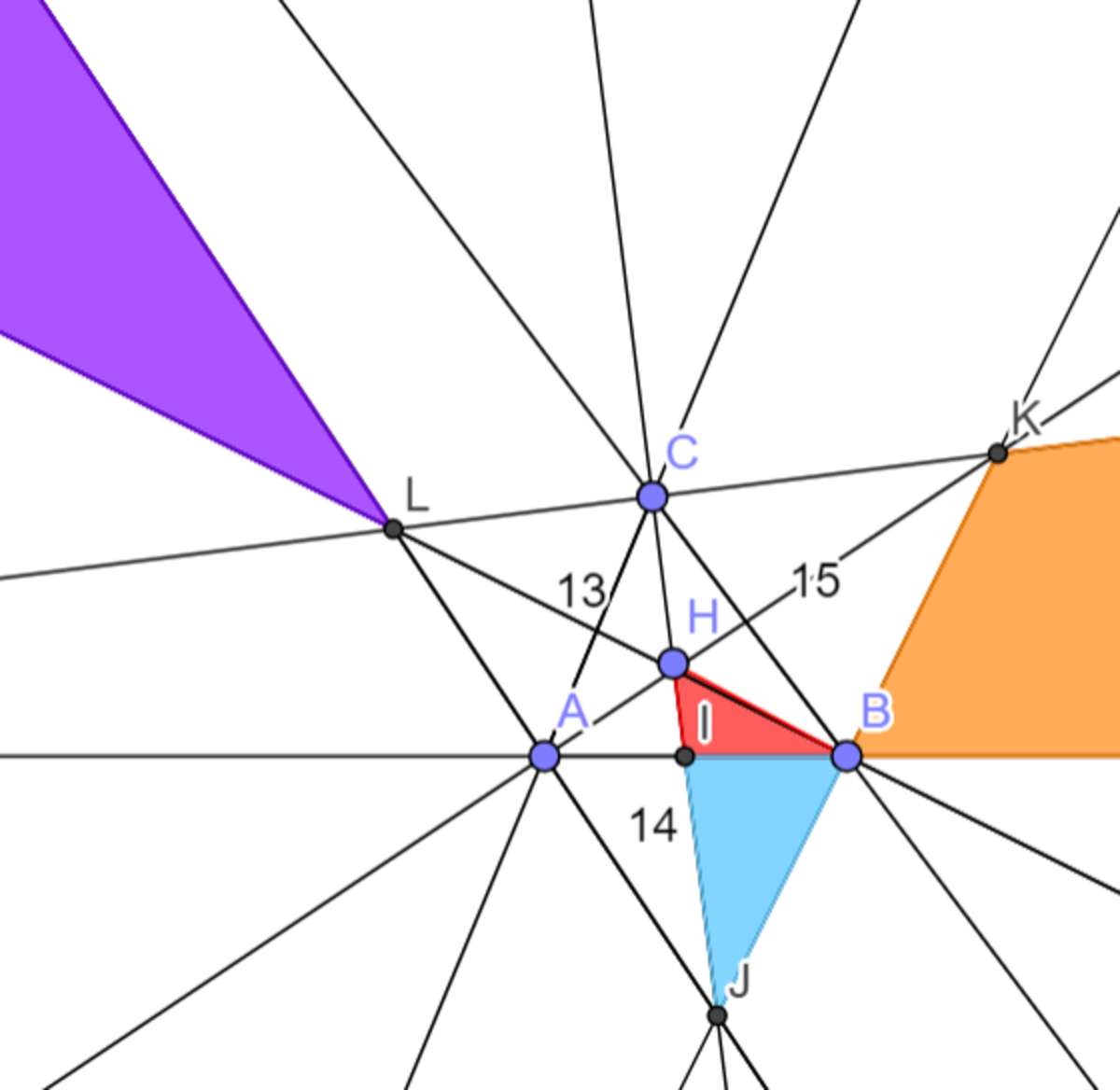

The colored regions are the regions which satisfy the requirements

$\textbf{But}$

The area of the purple region and the orange region is infinite and this can be shown.

The area of the purple region can be defined by the bisectors of exterior angles of $\angle A$ and the interior angle of $\angle B$ .

The bisectors of exterior angles of $\angle A$ and the interior angle of $\angle B$ do not meet again apart from at the point $L$ only.

Therefore, we conclude that the area of purple region is infinite!

The area of the orange region can be defined by the extended line of $AB$ and the exterior angle of $\angle C$ .

Suppose that the bisector of exterior angle of $C$ meet extended line of $AB$ at $T$

Then, we have

$\cfrac{AC}{CB}=\cfrac{AT}{TB}$

$\cfrac{AT}{TB}=\cfrac{13}{15}$

This indicates that $AT<BT$

But we know that $AT>BT$ , which leads to contradiction.

$\therefore$ the bisector of exterior angle of $C$ do not meet extended line of $AB$ .

Therefore, we conclude that the area of orange region is infinite!

Hunt for that Region!

The answer is 60.

1 solution

0 pending reports