Hunt for that Region! 2.0
As shown, A B = 4 5 , B C = 6 0 , A C = 7 5 in △ A B C .
Find the area of the region enclosed by the traces of P moving inside △ A B C , satisfying ( Area of △ P A B ) > ( Area of △ P B C ) > ( Area of △ P A C ) .
You can try a similiar problem here.
This is part of the set Things Get Harder! .
The answer is 225.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Wow, linear programming. Bravo! I did not see that coming. Well done!
@Nikola Yanakiev
Hold on. You might want to take a look at inequality 2. The inequality 2 you wrote corresponds to area of
Δ
P
A
C
>
area of
Δ
P
B
C
. Hope u would amend that a bit.
Log in to reply
Thank you for your comment! The solution has now been fixed.
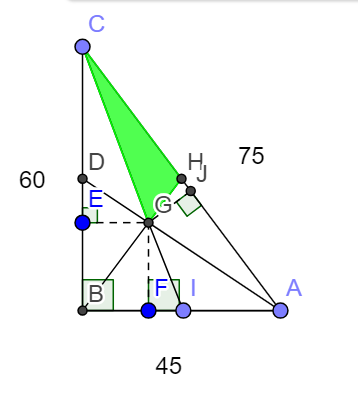
In the diagram above, point G is defined such that area of Δ G A B = area of Δ G B C = area of Δ G A C
The desired region is the green triangle Δ C G H .
Area of Δ A B C = 2 4 5 ⋅ 6 0 = 1 3 5 0
area of Δ G A B = area of Δ G B C = area of Δ G A C = 3 1 3 5 0 = 4 5 0
2 1 ⋅ G F ⋅ 4 5 = 2 1 ⋅ G E ⋅ 6 0 = 2 1 ⋅ G J ⋅ 7 5 = 4 5 0
G F = 2 0 , G E = 1 5 , G J = 1 2
E B F G is a rectangle.
∴ E B = G F = 2 0
tan ∠ E B G = E B G E = 2 0 1 5 = 4 3
tan ∠ B C A = 6 0 4 5 = 4 3
∠ G H J = ∠ E B G + ∠ B C A
∴ tan ∠ G H J = tan ( ∠ E B G + ∠ B C A ) = 1 − ( 4 3 ) 2 4 3 + 4 3 = 1 6 7 2 3 = 2 3 ⋅ 7 1 6 = 7 2 4
tan ∠ G H J = H J G J = 7 2 4
H J 1 2 = 7 2 4
H J = 2 4 1 2 ⋅ 7 = 2 7
C E + E B = C B
C E = 6 0 − 2 0 = 4 0
By Pythagorean Theorem ,
C E 2 + G E 2 = C G 2
G J 2 + C J 2 = C G 2
∴ C E 2 + G E 2 = G J 2 + C J 2
4 0 2 + 1 5 2 = C J 2 + 1 2 2
C J 2 = 4 0 2 + ( 1 5 2 − 1 2 2 ) = 4 0 2 + 9 2 = 4 1 2
C J = 4 1
C J = C H + H J
C H = 4 1 − 2 7 = 2 7 5
∴ Area of desired region = Area of Δ C G H = 2 1 ⋅ 2 7 5 ⋅ 1 2 = 2 2 5
Realizing that the given figure is a right triangle, we could solve the problem graphically quite easily. First we place the triangle in a cartesian coordinate system as so:
We pick a random point P = ( x , y ) where x = P x and y = P y . From the illustration the mentioned areas could be written as:
S △ P A B = 2 4 5 y
S △ P B C = 2 6 0 x
S △ P A C = S △ A B C − S △ P B C − S △ P A B = 2 4 5 ∗ 6 0 − 2 6 0 x − 2 4 5 y
Rearranging and solving the given inequalities we get:
9 0 y > 4 5 ∗ 6 0 − 6 0 x ⇒ 2 x + 3 y > 9 0 ( 1 )
4 5 ∗ 6 0 − 4 5 y < 1 2 0 x ⇒ 8 x + 3 y > 1 8 0 ( 2 )
4 5 y > 6 0 x ⇒ 3 y > 4 x ( 3 )
Since both ( 1 ) and ( 2 ) are linear inequalities we could easily find their solutions on the coordinate system using the extreme cases. Consequently the region that satisfies ( 1 ) is the area ( w i t h g r e e n ) above the line y = − 3 2 x + 3 0 , for ( 2 ) it is the area ( w i t h o r a n g e ) under y = − 3 8 x + 6 0 , for ( 3 ) - the p u r p l e region above line y = 3 4 x .
It so happens that all three functions intersect at one point D. The region that we are looking for is △ C E D . We find the coordinates of point D by putting the functions of the aforementioned lines equal to each other :
− 3 2 x + 3 0 = − 3 8 x + 6 0 ⇒ 2 x = 3 0 ⇒ D = ( 1 5 , 2 0 ) .
Point E is the intersection between C A and y = 3 4 x . Therefore the x coordinate of E is the solution to the equation − 3 4 x + 6 0 = 3 4 x ⇒ x E = 2 2 . 5 ; y E = 3 0 ⇒ C E = 3 7 . 5 . The distance from point D to C A can be found using the already mentioned formulas for the three areas. It turns out to be equal to 12. Finally, we can calculate the formula using the formula 2 C E ∗ 1 2 = 2 2 5
P.S. Looking into the illustration I've provided above, it turns out that the point D is the center of mass of the triangle. This gives insight into a more elegant solution to the problem. Let P be a random point in the triangle and C P ∩ B A = M . The ratio between S △ P B C and S △ P A C is just M A B M . In order for that to be greater than one (this is what the problem implies) point M has to be in the right half of BA. In other words every point on a line to the right of the median from point C provides us with a solution to one of the inequalities. Doing this for all medians/inequalities, the area in question once again turns out to be △ C E D . Using ratios S △ C E D = 2 1 ∗ S △ C D A = 2 1 ∗ 3 2 ∗ S △ C N A (point N is the midpoint of BA) = 2 1 ∗ 3 2 ∗ 2 1 ∗ S △ C B A = 6 1 ∗ S △ C B A = 2 2 5 .