Hybrid Ellipse Area

Calculus Level 5

Let's define two ellipses.

Ellipse 1:

$\frac{x^2}{9} + \frac{y^2}{1} = 1$

Ellipse 2:

$\frac{x^2}{1} + \frac{y^2}{9} = 1$

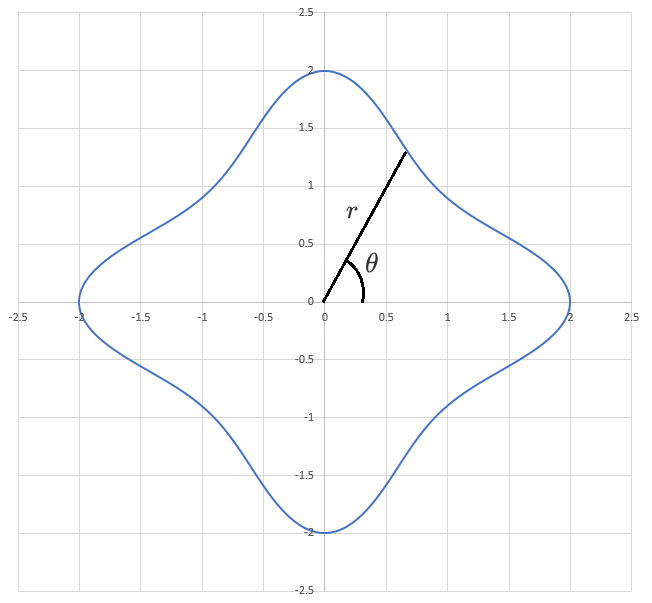
We could represent each ellipse in polar coordinates $(r,\theta)$ , where the radius and angle are defined as indicated in the image. The radii of Ellipse 1 and Ellipse 2 would be denoted as $r_1(\theta)$ and $r_2(\theta)$ .

Define "Ellipse" 3 as follows:

$r_3(\theta) = \frac{1}{2} r_1(\theta) + \frac{1}{2} r_2(\theta)$

What is the ratio of the internal area of "Ellipse" 3 to the internal area of Ellipse 1 (to 3 decimal places)?

Note: "Ellipse" 3 is not actually an ellipse, but is designated as such for convenience.

The answer is 0.881.

1 solution

Nicola Mignoni
Feb 18, 2018

Both ellipses can be written in polar coordinates

$\displaystyle \frac{x^2}{9}+y^2=1$ ,

$\displaystyle \frac{r^2\cos^2{\theta}}{9}+r^2\sin^2{\theta}=1$

Same job for the second ellipse and we get

$\displaystyle r_1(\theta)=\sqrt{\frac{9}{\cos^2{\theta}+9\sin^2{\theta}}}$

$\displaystyle r_2(\theta)=\sqrt{\frac{9}{9\cos^2{\theta}+\sin^2{\theta}}}$ .

So, we can write the requested function

$\displaystyle r_3(\theta)=\frac{1}{2}r_1(\theta)+\frac{1}{2}r_2(\theta)=\frac{1}{2}\sqrt{\frac{9}{\cos^2{\theta}+9\sin^2{\theta}}}+\frac{1}{2}\sqrt{\frac{9}{9\cos^2{\theta}+\sin^2{\theta}}}$

Now, the curve showed in picture can be written as

$\displaystyle c(\theta)=(r_3(\theta)\cos{\theta},r_3(\theta)\sin{\theta})$

Analitycally, the area enclosed by $c(\theta)$ is

$\displaystyle Area(c(\theta))=\int_{0}^{2\pi} f(\theta)dx(\theta)$ ,

where $f(\theta)=r_3(\theta)\sin{\theta}$ and $x(\theta)=r_3(\theta)\cos(\theta)$

Via numerical approach, $Area(c(\theta))\approx 8.311$ . The area of the ellipse is

$\displaystyle Area(Ellipse)=2\int_{-3}^{3} \sqrt{1-\frac{x^2}{9}}dx=3\pi$ . Eventually, the ratio results $\approx 0.881$ .

Hybrid Ellipse Area

The answer is 0.881.

1 solution

0 pending reports