Hydroelectric power plant
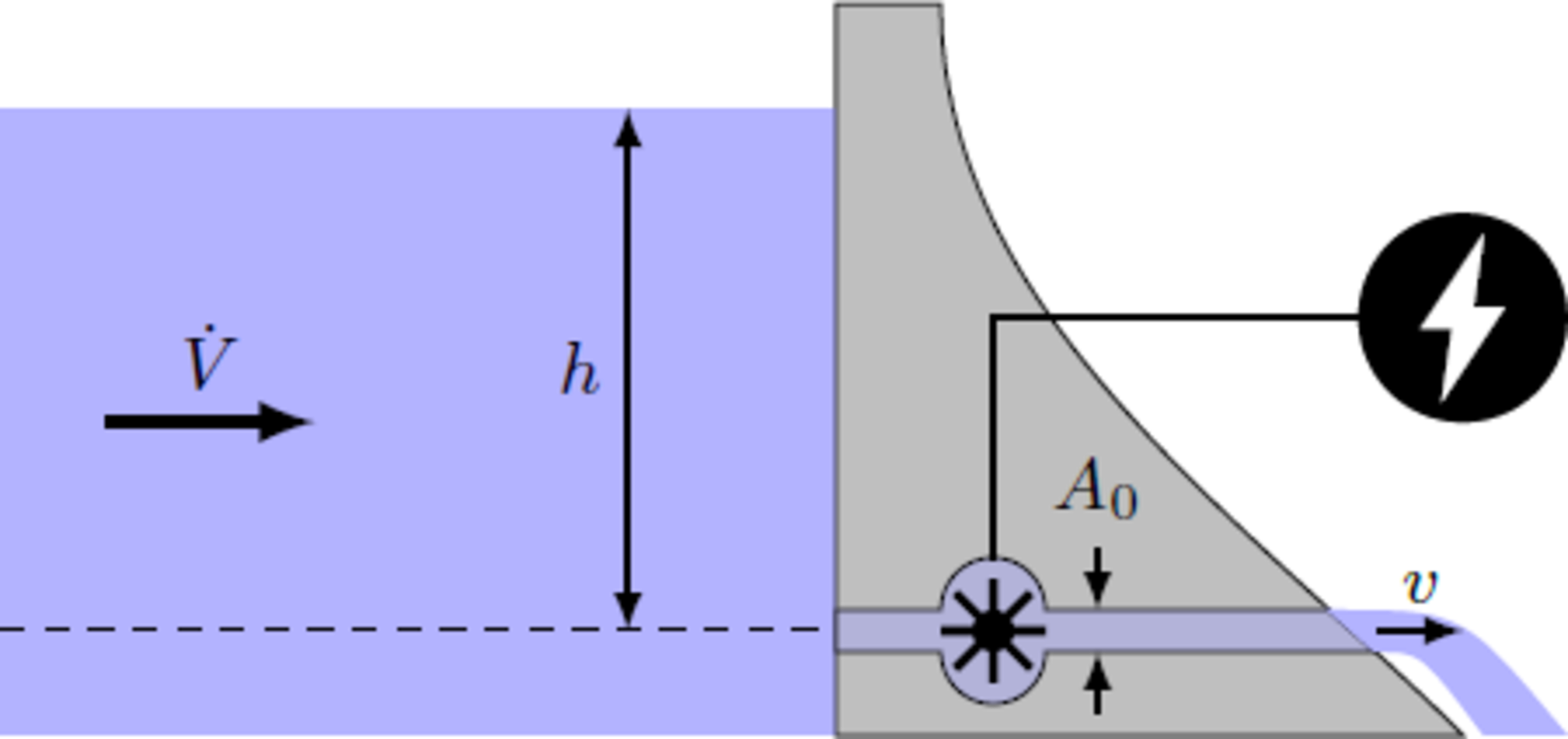
A river with a volume flow of is dammed up to generate electricity. The water from the bottom of the reservoir is directed through a pipe with the cross-sectional area to the turbines. The turbines of the power plant have an efficiency of . How much power in megawatts does the plant produce?
Assumptions : Approximate the density of water by and the gravitional constant by .
The answer is 108.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
In equilibrium, the outflow must correspond to the inlet, so that we can caculate the flow velocity v in the pipe: A 0 v = V ˙ ⇒ v = A 0 V ˙ = 6 s m On the other hand, energy conservation must be assured, so that the potential energy of the water volume Δ V with mass Δ m = ρ Δ V is converted into kinetic and electric energy: ⇒ ⇒ U Δ m g h h = T + W el = 2 1 Δ m v 2 + η Δ m g h = 2 ( 1 − η ) v 2 = 9 0 m With the height h of the reservoir, we can estimate the electrical power of the plant to P = η ρ V ˙ g h = 0 . 8 ⋅ 1 0 0 0 ⋅ 1 5 0 ⋅ 1 0 ⋅ 9 0 W = 1 0 8 MW