Hyper-intriguing Ornament IV

Geometry Level 4

Consider the hyperball $\sum_{i=1}^{n}{x_i}^2 \leq 9$ and the hypercube $\left[-2,2 \right]^n$ in $\mathbb{R}^n$ . Find the limit of the percentage of the hypercube (by $n$ -volume) that resides outside the hyperball, as $n \rightarrow \infty$ ? Round your answer to the nearest integer.

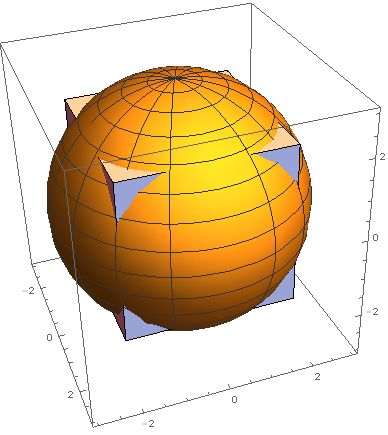
The figure illustrates the case $n=3$ .

The figure and the idea are stolen from Comrade Huan Bui.

0 37 100 32 93 None of the others

1 solution

Otto Bretscher
Dec 30, 2018

Surprisingly perhaps, the volume of an $n$ -ball with a fixed radius goes to 0 as $n\rightarrow \infty$ , as discussed here . (There are somewhat straightforward ways to demonstrate this fact, and I will be glad to offer such an explanation upon request.) Since the volume of the hypercube $[-2,2]^n$ grows without bound, the percentage of the hypercube that resides outside the hyperball will approach $\boxed{100}$ .

Hyper-intriguing Ornament IV

1 solution

0 pending reports