Hyperbola and the angle bisector
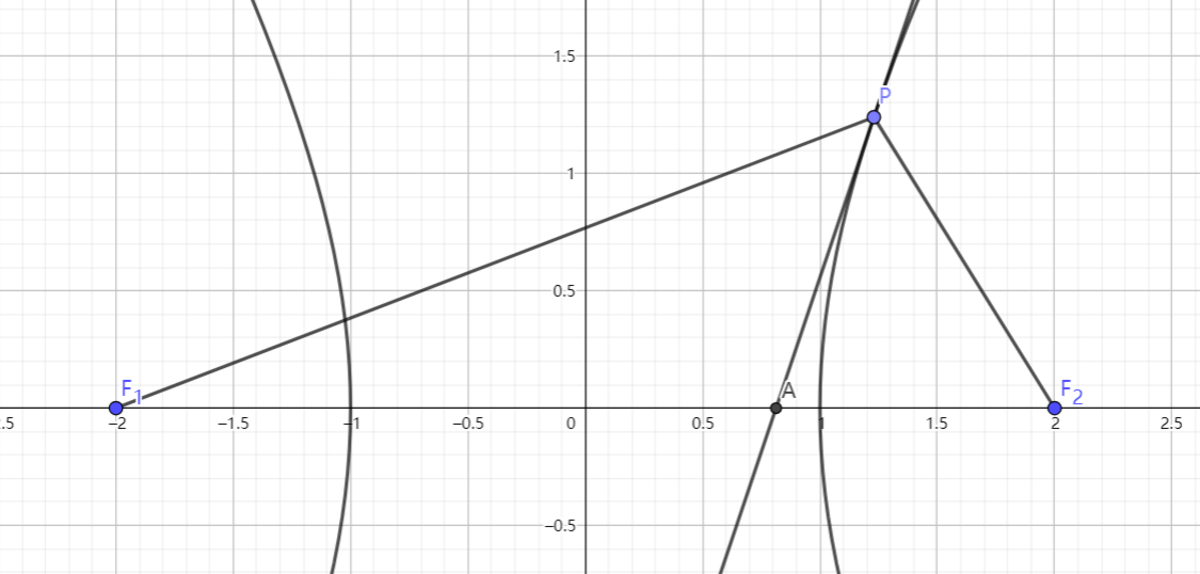
Given that hyperbola x 2 − 3 y 2 = 1 has left focus F 1 and right focus F 2 . Point P on the hyperbola is such that ∠ F 1 P F 2 = 3 2 π . The angle bisector of ∠ F 1 P F 2 intersects the x -axis at point A .
Find the length of P A .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
I did the same thing as you, only difference is I took parametric form of the point, i.e, (sec,1.732tan). My keypad sucks so I had to type approximate value of square root of 3
Let the x -coordinate of P be p . Since P is on the hyperbola x 2 − 3 y 2 = 1 , its y -coordinate is 3 p 2 − 3 .
Let B be the intersection of the line through P perpendicular to F 1 F 2 . Then B F 1 = p + 2 , B F 2 = 2 − p , and B P = 3 p 2 − 3 , and by the Pythagorean theorem on △ P B F 1 and △ P B F 2 , P F 1 = ( p + 2 ) 2 + 3 p 2 − 3 = 2 p + 1 and P F 2 = ( 2 − p ) 2 + 3 p 2 − 3 = 2 p − 1 .
By the law of cosines on △ P F 1 F 2 , 4 2 = ( 2 p + 1 ) 2 + ( 2 p − 1 ) 2 − 2 ( 2 p + 1 ) ( 2 p + 1 ) cos 3 2 π , which solves to p = 2 5 for p > 0 . Therefore, P F 1 = 2 ( 2 5 ) + 1 = 5 + 1 and P F 2 = 2 ( 2 5 ) − 1 = 5 − 1 .
The length of an angle bisector d of a triangle is d 2 = b c − ( b + c ) 2 a 2 b c , so ∣ P A ∣ = ( 5 + 1 ) ( 5 − 1 ) − ( 5 + 1 + 5 − 1 ) 2 4 2 ( 5 + 1 ) ( 5 − 1 ) = 5 2 5 .
It should be noted that the angle bisector P A of ∠ F 1 P F 2 is actually tangential to the hyperbola at P (see note). For hyperbola a 2 x 2 − b 2 y 2 = 1 , the tangent at P ( x 0 , y 0 ) is given by a 2 x 0 x − b 2 y 0 y = 1 . For A ( x A , 0 ) , ⟹ x A = x 0 a 2 . Then ∣ P A ∣ = ( x 0 − x 0 a 2 ) 2 + y 0 2 .
To find x 0 and y 0 , let F 1 ( − c , 0 ) and F 2 ( c , 0 ) . Then
1 − y 0 2 c 2 − x 0 2 y c + x 0 0 + y c − x 0 0 y 0 2 − c 2 + x 0 2 2 c y 0 y 0 2 − c 2 + b 2 a 2 y 0 2 + a 2 2 c y 0 4 3 y 0 2 + 1 2 y 0 − 9 3 ⟹ y 0 ⟹ x 0 ⟹ ∣ P A ∣ = tan 3 2 π = − 3 = − 3 = 0 = 2 3 = 1 + 3 y 0 2 = 2 5 = ( x 0 − x 0 1 ) 2 + y 0 2 = 5 2 5 Putting a = 1 , b = 3 , c = 2
Note: I am not able to come up with a general proof but we can see that when P is at the vertex ( a , 0 ) , ∠ F 2 P F 2 = π and the tangent is vertical. And when P ( ∞ , ∞ ) , the tangent is parallel to the asymptote.
Let P ( x , y ) be its coordinate, then we have x 2 − 3 y 2 = 1 ⟹ y 2 = 3 x 2 − 3 .
Since ∠ F 1 P F 2 = 2 π / 3 , using Cosine Law we have 1 6 = F 1 F 2 2 = P F 1 2 + P F 2 2 − 2 P F 1 ⋅ P F 2 cos ( 3 2 π ) = P F 1 2 + P F 2 2 + P F 1 ⋅ P F 2 .
By P F 1 2 = ( x + 2 ) 2 + y 2 , P F 2 2 = ( x − 2 ) 2 + y 2 ,
we have 1 6 ∴ x = ( x + 2 ) 2 + y 2 + ( x − 2 ) 2 + y 2 + ( x + 2 ) 2 + y 2 ( x − 2 ) 2 + y 2 = 2 x 2 + 8 + 2 y 2 + ( x + 2 ) 2 + 3 x 2 − 3 ( x − 2 ) 2 + 3 x 2 − 3 = 2 x 2 + 8 + 2 ( 3 x 2 − 3 ) + 4 x 2 + 4 x + 1 4 x 2 − 4 x + 1 = 8 x 2 + 2 + ( 2 x + 1 ) ( 2 x − 1 ) because x > 1 = 1 2 x 2 + 1 = 2 5 .
It is pretty lucky that the terms in square root is a perfect square! By apply y 2 = 3 x 2 − 3 we find y = 3 / 2 .
From this we find P F 1 = 5 + 1 , P F 2 = 5 − 1 . Since P A is the angle bisector of ∠ F 1 P F 2 , using area argument we find P F 2 P F 1 = A F 2 A F 1 ,
Using A F 2 as the sole variable here, we find A F 2 = 5 1 0 − 2 5 . Therefore the x -coordinate of A is 2 − 5 1 0 − 2 5 = 5 2 5 ,
Using P ( 5 / 2 , 3 / 2 ) , A ( 2 5 / 5 , 0 ) , we get P A = 5 2 5 .
Note: This also shows that Δ A P F 2 is equilateral.
Eccentricity of the hyperbola is 1 + 3 = 2 . So the coordinates of F 1 and F 2 are ( − 2 , 0 ) and ( 2 , 0 ) respectively. Let the coordinates of P and A be ( h , k ) and ( a , 0 ) respectively. Then slopes of the line segments P F 1 , P F 2 and P A are h + 2 k , h − 2 k and h − a k respectively. So we have
h 2 − 3 k 2 = 1
tan 3 2 π = − 3 = 1 + h 2 − 4 k 2 h − 2 k − h + 2 k
tan 3 π = 3 = 1 + ( h − a ) ( h + 2 ) k 2 h − a k − h + 2 k .
From the first two equations we get h = 2 5 , k = 2 3 .
Substituting the values of h and k in the third equation we get a = 5 2 and ∣ P A ∣ = ( h − a ) 2 + k 2 = 5 2 = 5 2 5 .