Hyperbolic Cliffs
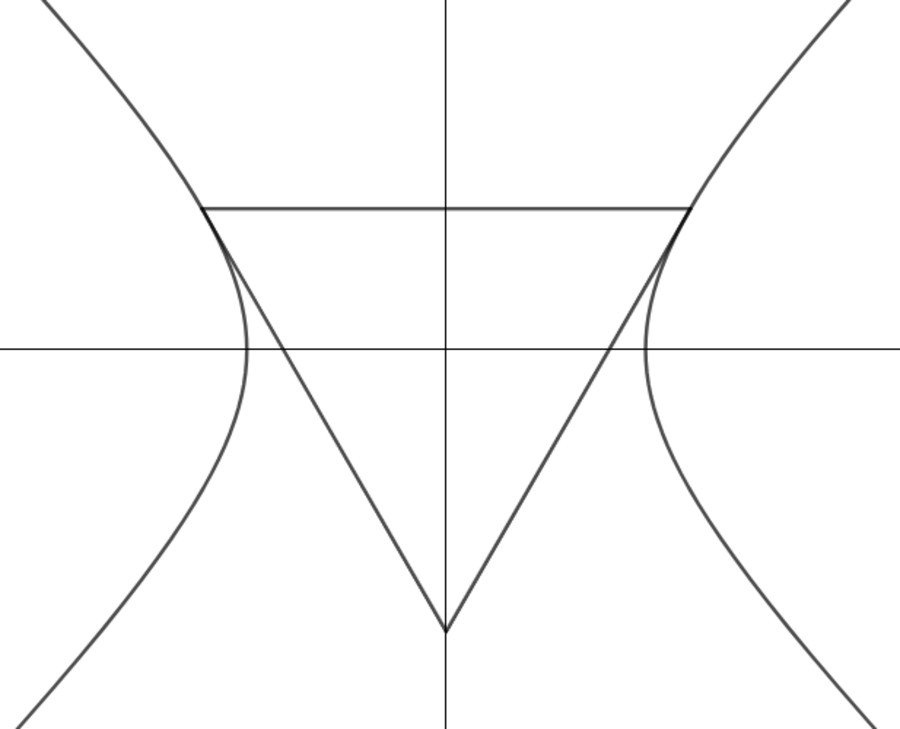
In the rectangular plane, an equilateral triangle whose incenter exists at the origin touches both sides of the hyperbola represented by the equation x 2 − y 2 = 1 , each exactly at one point. It can be shown that the maximum possible area of the equilateral triangle can be presented by
B A C
where A , B and C are positive integers, g cd ( A , B ) = 1 and C square-free. Find the value of A + B + C .
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
If we divide the equilateral triangle into 6 parts by its heights, it's clear that x = √3y leading to y = 1/√2 and x = √(3/2) when plugged into x² – y² = 1.
Max area
= 6 × little right triangle's area
= 6 × (1/2) × √(3/2) × √(1/2)
= 3√3/2
Answer = 3 + 2 + 3 = 8
By symmetry, the right side of the equilateral triangle will follow the equation y = 3 x + b , where b is the y -intercept.
Substituting this into x 2 − y 2 = 1 gives x 2 − ( 3 x + b ) 2 = 1 , which rearranges to x = 2 1 ( − 3 b ± b 2 − 2 ) .
Since the equilateral triangle touches the hyperbola at exactly one point, there is only one answer for x , so b 2 − 2 = 0 , which means b = − 2 for b < 0 .
The circumradius of the equilateral triangle is R = ∣ b ∣ = 2 , and the area of the equilateral triangle is A = 3 ⋅ 2 1 R 2 sin 1 2 0 ° = 2 3 3 .
Therefore, A = 3 , B = 2 , C = 3 , and A + B + C = 8 .
Let the variable equilateral triangle be A B C , M be the midpoint of the horizontal side A B , and r be the radius of the incircle. Since △ A B C is equilateral, its incenter is also its centroid. Then M C = 3 r , vertex C = ( 0 , − 2 r , and the equation of B C is given by:
x y + 2 r = 3 ⟹ y = 3 x − 2 r
At the point P on the hyperbola, where B C is tangent to, has a gradient same as the line B C , which is 3 . Then we have:
2 x − 2 y d x d y ⟹ d x d y y x ⟹ x = 0 = y x = 3 = 3 y When gradient d x d y = 3
Substitute x = 3 y in the B C line equation, y = 3 y − 2 r ⟹ y = r . This means that the tangent point P coincides with B . Then x = 3 r . Substitute in the hyperbola equation, 3 r 2 − r 2 = 1 ⟹ r = 2 1 . And the area of △ A B C is 2 1 ⋅ 2 x ⋅ 3 r = 3 3 r 2 = 2 3 3 . The required answer is A + B + C = 3 + 2 + 3 = 8 .