Hyperbolic Conic Section
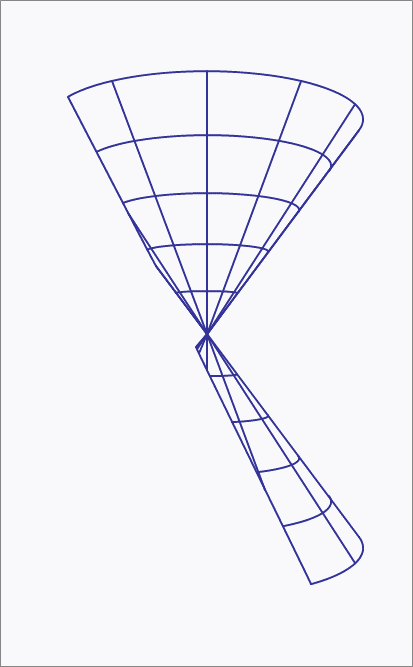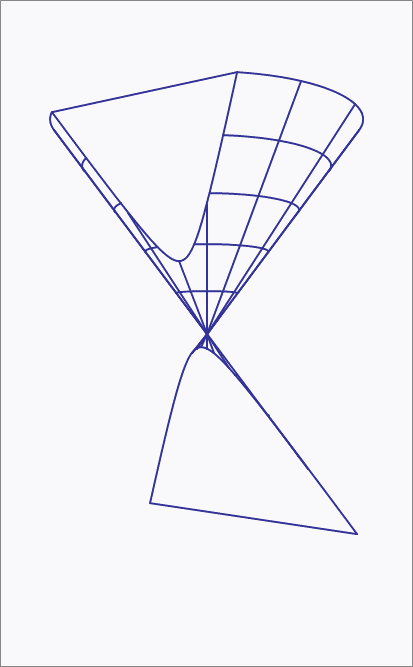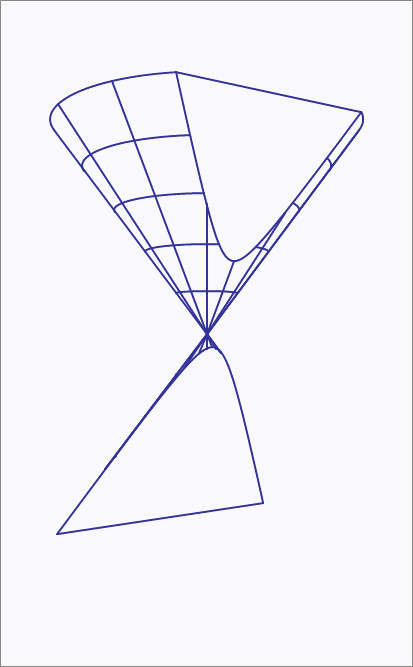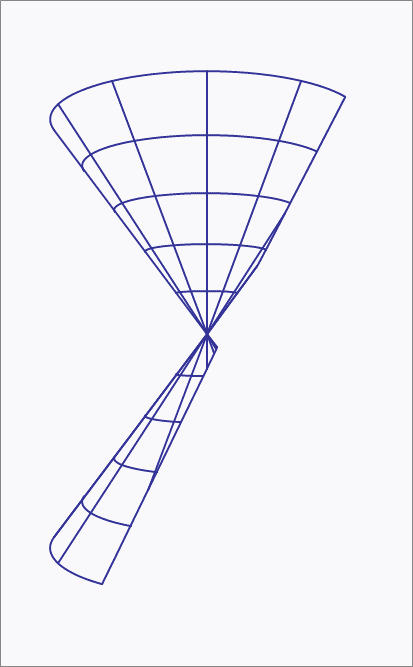
A twin cone has the angle between its curved surface and its axis equal to . The axis of the twin cone system is along the z-axis, and its vertex is at the origin. A plane having the equation
intersects with the twin cones. We are given that and that and that . With these values for and , the intersection is a hyperbola. By attaching a reference frame - to the cutting plane and choosing its origin to be at the center of the hyperbola, and also choosing its orientation appropriately, with the -axis lying parallel to the -plane and the -axis running up the cutting plane, the resulting hyperbola has the following equation
The center of the hyperbola is at the point for positive and . Find the value of .
The answer is 242.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
There is a formula for the eccentricity of the conic section resulting from a cutting plane intersecting a cone whose axis is vertical (i.e. along the z-axis).
e = sin α sin β
where β is the angle that the cutting plane makes with the horizontal plane, and α is the angle that the curved surface makes with the horizontal plane. This is illustrated in the image below.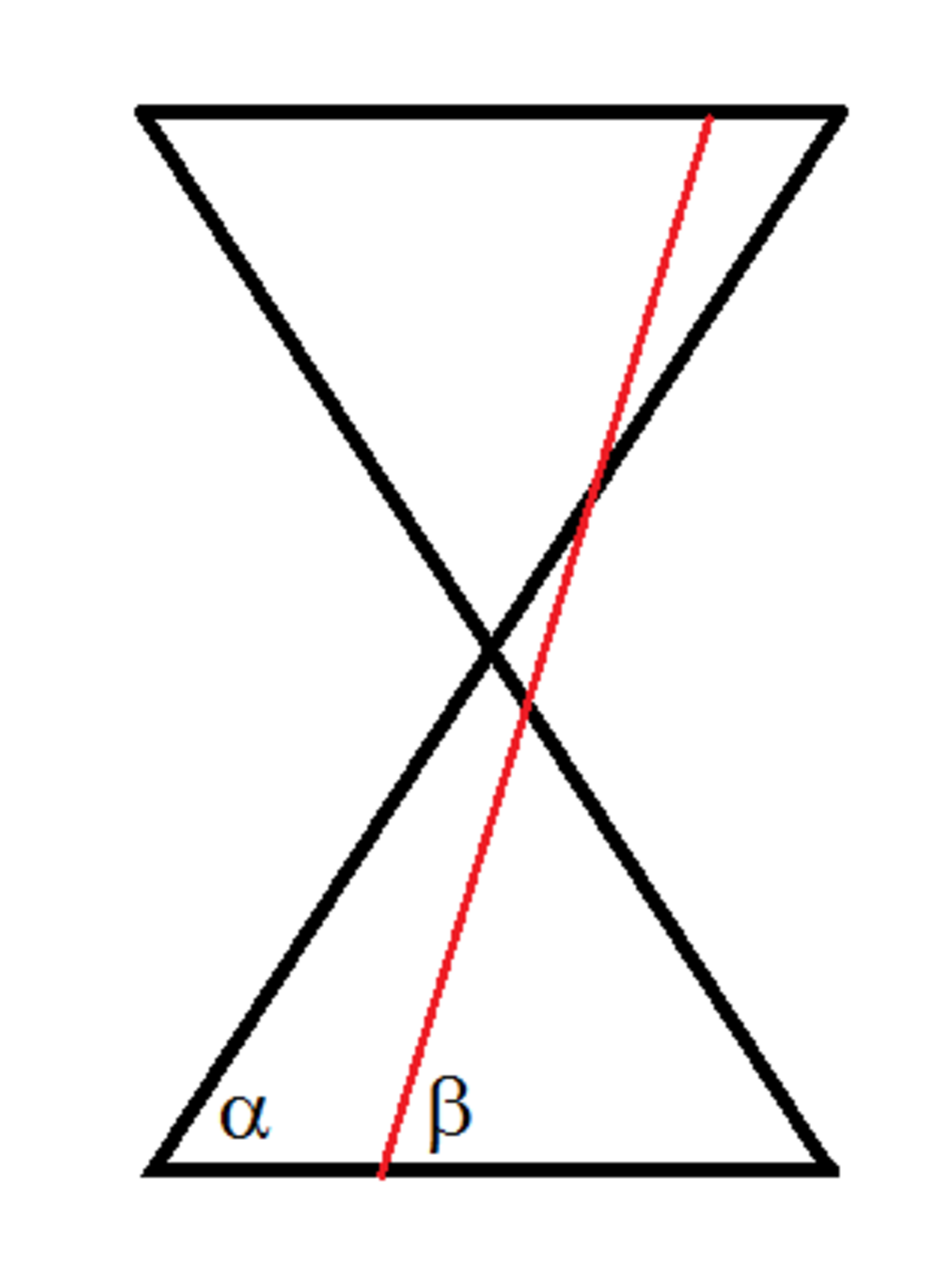
Note that α = 2 π − θ c , and that β = θ p .
Hence the eccentricity of the resulting conic section is,
e = cos ( θ c ) sin ( tan − 1 ( 2 ) ) = 5 4 5 2 = 2 5
Now the eccentricity e is related to a and b (in the problem) as follows:
e 2 = 1 + a 2 b 2
Substituting the value of e results in
a b = 2 1
Next we find a from the intersection of the cutting plane with the cone in the x z plane.
We have two lines from the cone, given by z = tan ( α ) x and z = − tan ( α ) x . These intersect with the line z = tan ( θ p ) ( x − x 0 ) at ( x 1 , y 1 ) and ( x 2 , y 2 ) , respectively, where,
x 1 = x 0 tan ( θ p ) / ( tan ( θ p ) − tan ( α ) ) , and
x 2 = x 0 tan ( θ p ) / ( tan ( θ p ) + tan ( α ) )
Substituting tan ( θ p ) = 2 and tan ( α ) = 3 4 , we get,
x 1 = 1 5 and x 2 = 3 . Corresponding to this, we have,
y 1 = x 1 tan ( α ) = 2 0 , and y 2 = − x 2 tan ( α ) = − 4 .
The distance between these two points that we just found is twice a . Therefore,
2 a = ( 1 5 − 3 ) 2 + ( 2 0 + 4 ) 2 , i.e. a = 6 5
Thus, a 2 = 1 8 0 , and b 2 = 4 1 a 2 = 4 5
The center is midpoint of the two points of intersection that we found.
Center = 2 1 ( ( 1 5 , 0 , 2 0 ) + ( 3 , 0 , − 4 ) ) = ( 9 , 0 , 8 )
This makes the answer 1 8 0 + 4 5 + 9 + 8 = 2 4 2