Hypercube Faces
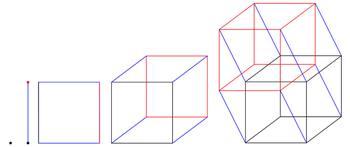
How many 2-dimensional faces does a tesseract (4-dimensional cube) have?
Note: A face is a flat 2-dimensional surface that is part of the boundary of a polyhedral object.
The answer is 24.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Generalize even further. The number of A-dimensional "faces" (e.g. 0-dimensional faces being vertices, 1-dm faces being edges, 3-dimensional faces being cubes etc.) of an N-dimensional cube is given by:
Z A ∣ N = 2 N − A ( A N )
I once worked on the hypernization of platonic solids. I have a similar general formula for N-dimensional tetraeders and N-dimensional octaeders. If you're interested let me know.
Log in to reply
The generalization of the generalization is why I wrote the n choose 2 format as opposed to just using the explicit formula (1/2)(n)(n-1).
C(n,2) * 2^n / 4
C(n,2)*2^(n-2)= the number of faces on a nth dimensional tesseract
(nc2*2^n)/n ?
From 2 dimensions to 3 dimensions the square was copied and each edge of the square became a face. 2 face's for the square that gets copied and 4 new faces for each edge of the square which gives you 6 faces. Going a step up from 3 dimensions to 4 dimensions you do the same. 6 faces of the original cube that gets multiplied by 2 plus a face for each edge's of the cube which is 12. 12+12= 24 and you have your answer. 24 faces
Vertices are easy to count: each dimension doubles the number. Dimension 1 has 2, dimension 2 has 4, dimension 3 has 8, and dimension 4 has 16. In general for an n -dimensional cube there are 2 n vertices.
Now, let's look at faces. We'll consider the 3-dimensional cube first as an example:
On the cube, each vertex is adjacent to 3 faces. We can justify this with coordinates; suppose one vertex of a unit cube is at (0, 0, 0) with the diagonal across the cube at (1, 1, 1). If we travel diagonally across each face, it represents changing two of the coordinate values from 0 to 1. That is, the possible diagonals of faces are from (0, 0, 0) to (1, 1, 0), (1, 0, 1) and (0, 1, 1). Since we're counting the number of ways to turn 2 of the coordinates into 1, that's equivalent to ( 2 3 ) = 3 .
Now let's count how many faces each vertex on the tesseract is adjacent to; again, consider one vertex oriented at (0, 0, 0, 0) with the diagonal across the hypercube at (1, 1, 1, 1). Once again the diagonal across a face is represented by changing two of the 0 values to 1; so the number of adjacent faces is ( 2 4 ) = 6 . (Explicitly, the values are (1, 1, 0, 0), (1, 0, 1, 0), (1, 0, 0, 1), (0, 1, 1, 0), (0, 1, 0, 1) and (0, 0, 1, 1).)
Multiplying the 16 vertices by the number of adjacent faces gets 1 6 × 6 = 9 6 . Note however we have overcounted by a factor of 4 because each face has 4 vertices adjacent. So the final count of faces is 9 6 / 4 = 2 4 .
BONUS: Can you generalize this into a formula for the number of faces of n -dimensional cubes?