Hyperdrive accident
On the interstellar highway there was a dramatic accident where a human pilot (blue spaceship) collided with a robot (red spaceship), that drived on the wrong way. From the viewpoint of a stationary witness, both spaceships were traveling parallel to the axis at velocities and , respectively ( is the light velocity). The space ship of the human pilot had been equipped with a radar system capable to locate other spaceships up to a range of (Ls is the light second). How much time did the pilot have to avoid the ghost driver (in units of seconds)?
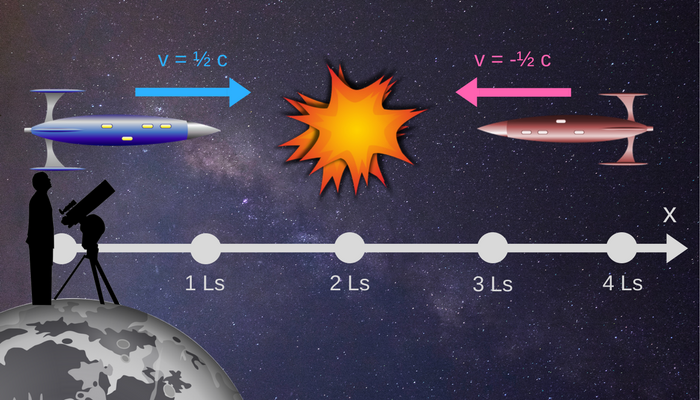
Note: The world lines of the two spaceships can be seen as a straight line in the -diagram (Minkowski diagram), starting from the points and to the point of the collision. The length unit in both directions is .

For the construction of the diagram from the perspective of the spacecraft pilot, we must note the following:
-
The coordinate axes for and of the pilot are inclined (from the perspective of the witness) by an angle , so that the unit cell is deformed into a parallelogram. The angle is fixed by In particular, the world line of the pilot represents the axis.
-
The unit length in the reference system of the pilot is stretched so that In this way, the parallelogram with side length has the same area as the corresponding square.
The answer is 1.00.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The base vectors for coordinate system of the pilot are a x ′ = a ′ ( cos α sin α ) , a t ′ = a ′ ( sin α cos α ) The coordinates ( x , c t ) and ( x ′ , c t ′ ) , that describe the same point X in spacetime, are connected by X ⇒ ( x c t ) = x a x + c t a t = x ′ a x ′ + c t ′ a t ′ = cos 2 α 1 ( cos α x ′ + sin α c t ′ sin α x ′ + cos α c t ′ ) = cos 2 α 1 ( cos α sin α sin α cos α ) ( x ′ c t ′ ) Inversion of a 2 × 2 matrix can be done as follows: ( a c b d ) − 1 = a d − b c 1 ( d − c − b a ) Therefore, ( x ′ c t ′ ) = cos 2 α 1 ( cos α − sin α − sin α cos α ) ( x c t ) = γ ( 1 − β − β 1 ) ( x c t ) with β = c v 1 = 2 1 and γ = 1 − β 2 1 = 3 2 . Therefore, the points B and C have the following coordinates in the moving reference frame ( x B ′ , c t B ′ ) ( x C ′ , c t C ′ ) = ( 3 8 , 3 − 4 ) = ( 0 , 3 6 ) We calculate the velocity of the incoming shaceship by v 2 ′ = t C ′ − t B ′ x C ′ − x B ′ = 6 − ( − 4 ) 0 − 8 c = 1 0 8 c = 0 . 8 c
Thus, the incoming spacecraft moves from the pilot's viewpoint with 80% of the light velocity. A radar pulse propagating at the speed of light is reflected at the point D at the distance x ′ = 4 Ls from the ghost driver and reaches after the time Δ t ′ = 4 s our pilot at point E . The ship controlled by a robot needs 4 Ls / ∣ v 2 ∣ = 5 s for the same route, so that the human pilot only has a warning period of one second.