Hyperloop: Curves
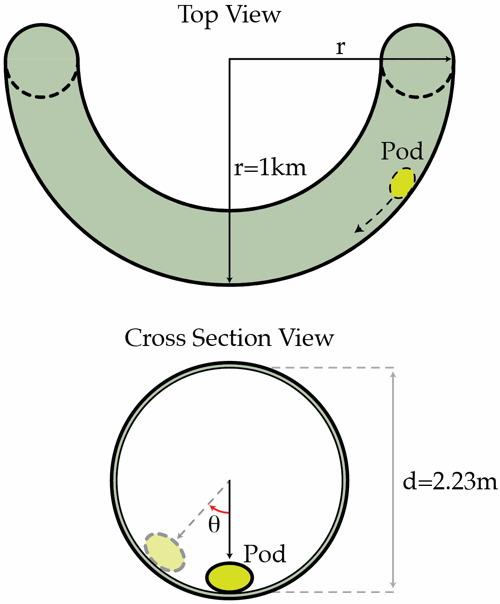
The Hyperloop is a hypothetical new fast transport system between cities, which works by launching pods that carry people through a very low air pressure tunnel. Consider a circular tunnel of diameter 2 . 2 3 m and a simple model of the Hyperloop pod as a point mass that usually travels at the bottom of the tunnel when it is straight. Tunnels can't always be straight, of course, so let us suppose that one section of the tunnel has a curve corresponding to an arc of a circle with radius 1 km .
What angle in degrees does the line drawn from the center of the tunnel to the pod make with the vertical axis if the pod is traveling at a constant 3 0 0 m/s along this curved section of the tunnel?
Details and assumptions
- The acceleration of gravity is − 9 . 8 m/s 2 .
- Ignore friction as the friction force on the Hyperloop is minimal.
The answer is 83.8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
Imagine the point mass (representing the pod) on the circumference of a circle (representing the tube). The point will experience a centripetal force in the horizontal direction (due to the curved nature of the tube) and will also be pulled down by its own weight in the vertical direction. The centripetal force will push the point up along the side of the circle, creating the offset angle we are looking for, which we will denote as θ , and also placing the point on a slanted plane tangent to the circle.
Now, we write the forces F c and F g in terms of their horizontal components with respect to the plane of the point. (The vertical components are balanced out by the normal force) F c H = F c sin ( 9 0 − θ ) F g H = F g sin θ Then, because forces are balanced, we can equate these two, yielding F c sin ( 9 0 − θ ) = F g sin θ r m v 2 sin ( 9 0 − θ ) = m g sin θ r v 2 sin ( 9 0 − θ ) = g sin θ Because sin ( 9 0 − θ ) = cos θ , we get r v 2 cos θ = g sin θ r g v 2 = tan θ Substituting v = 3 0 0 , r = 1 0 0 0 , and g = 9 . 8 gives us tan θ = 9 8 0 0 9 0 0 0 0 θ = arctan 9 8 0 0 9 0 0 0 0 = 8 3 . 8
The diameter of the cross section is small, hence quiet irrelevant to the solution(hence take r= 1000)
( m v 2 / r ) sin θ = m g cos θ
cot θ = v 2 / r g
Putting in the values, this simplifies to 83.8 degrees.
Equating centripetal force and horizontal resultant force:
F = r m v 2 = m g tan ( θ ) r v 2 = g tan ( θ ) tan ( θ ) = g r v 2 θ = tan − 1 ( g r v 2 ) = tan − 1 ( 9 . 8 × 1 0 0 0 3 0 0 2 ) = 8 3 . 7 8 5 6 ∘
The thing to note is that the radius/diameter of the tunnel does not matter since there is no motion in the vertical plane. The forces at work are gravity ( m g ) acting downwards and the centrifugal force ( m r ω 2 or m v 2 / r ) acting horizontally. The ball reaches a position on the tube where the forces tangential to the loop cancel each other.
So if θ is the angle that the line joining the center of the loop and the pod makes with the vertical, then we have:
m g cos ( π / 2 − θ ) = m r ω 2 cos θ ⇔ tan θ = g r v 2 ⇔ θ ≈ 8 3 . 7 8 6
Use the formula:
t a n ( t h e t a ) = v 2 / r g
t h e t a = a r c t a n ( 3 0 0 2 / 1 0 0 0 ∗ 9 , 8 )
t h e t a = a r c t a n ( 9 , 1 )
t h e t a = 8 3 . 8 0
The centrifugal acceleration experienced by the Hyperloop pod is 90 m/s^2 as calculated using a = v^2/r = 300^2/1000. The Hyperloop pod also experiences an accleration of 9.8 m/s^2 perpendicular to the other acceleration. The angle of the resultant acceleration and the vertical is the final answer. To calculate this you take the inverse tangent of 9.8/90 and then subtract the solution from 90 to obtain 83.8 degrees.
The angle, θ , is cos − 1 ( F c g ) , where F c = centripetal acceleration
θ = c o s − 1 ( ( r v 2 ) g ) = c o s − 1 ( v 2 g r )
θ = c o s − 1 ( 3 0 0 2 9 . 8 × 1 0 0 0 ) = 8 3 . 8 ∘
I'm using the following assumptions: The tunnel lies in a plane perpendicular to the force of gravity, and the curve is left or right. Not a great assumption given that we had to take the curvature of the earth into account for the previous question, but still :) And as the pod passes through the tunnel it will ride up the side due to the centripetal acceleration, and we are trying to calculate how far up the side it rides.
The centripetal acceleration can be calculated as a = r v 2 , i.e. 9 0 m s − 1 . If we consider the free body force diagram, we have m a in the horizontal direction, and m g in the vertical direction. Therefore cot θ = m a m g .
Plugging inverse cotangent of 9 0 9 . 8 into a calculator gives 8 3 . 7 8 5 6 . . . degrees.
I'm posting my solution as it is shorter than some of the others. Was I right to not mention the force against the side of the tunnel, or does it need to be considered?
I figured that whatever force the pod pushes against the tunnel with, the tunnel pushes back, so we don't need to take that into account.
We seek the asterisked angle θ . Let's start with a diagram of what we know...
The forces acting upon the capsule are:
If we resolve the reaction force parallel and perpendicular to the ground, we observe that R sin θ gives the centripetal force required to move in a circle. R cos θ balances the downward gravitational force.
Mathematically:
where v is the velocity of the capsule.
Dividing equation one by equation two gives...
tan θ = r × g v 2
Now from the question we know v = 3 0 0 s m , r = 1 0 0 0 m and g = 9 . 8 s 2 m
substituting in gives tan θ = 1 0 0 0 × 9 . 8 3 0 0 2
hence tan θ = 9 . 1 8 3 6 7 . . .
so θ = 8 3 . 7 9 ∘