Hypothetical Hydrostatics
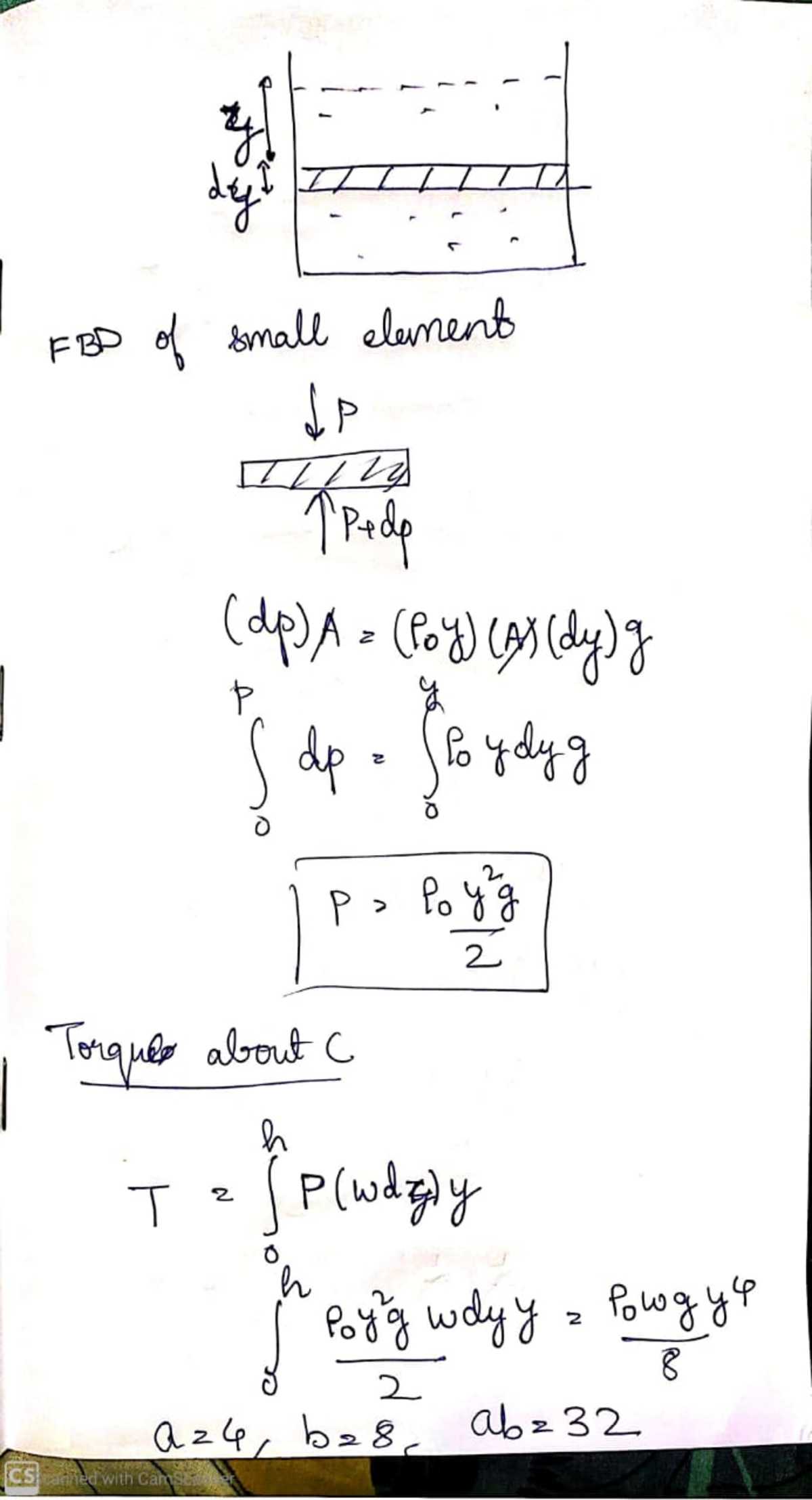
A cuboidal tank has a height of O A = h and a width of w (into the plane of the paper). The tank is filled to its brim O C by a hypothetical fluid whose density varies with the depth y according to ρ ( y ) = ρ 0 y , where ρ 0 is a constant of appropriate dimensions.
If the torque exerted on the wall C B about the point C by the fluid is given by:
T = b ρ 0 g w h a
where a and b are integers, find a b .
Details:
- The fluid in the tank is static.
- The tank is placed in a vacuum and an ambient gravity exists along the y direction.
The answer is 32.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Karan Chatrath , bro Can u please suggest which book should I prefer for quality concepts in wave optics for 11 and 12(IIT JEE)
Log in to reply
I am not the best person to seek advice from regarding JEE, but if you enjoy learning the subject and want to read about concepts, I would recommend searching for the Feynman Lectures. They are freely available on the internet.
For a compressible fluid whose density varies with depth, we cannot apply the pressure formula of p = ρ ( h ) g h or ( ρ ( y ) g y in this problem) directly. To find the pressure p ( y ) at a depth of y from the liquid surface, consider a column of the liquid of cross-sectional area A on top of a point at depth y . The weight of the column of liquid at this point is given by:
F g = ∫ 0 y ρ ( z ) A d z ⋅ g = g A ∫ 0 y ρ 0 z d z = 2 ρ 0 g A y 2
The pressure at a depth of y is:
p ( y ) = 2 A ρ 0 g A y 2 = 2 ρ 0 g y 2
And the torque exerted on wall C B about C is:
T = ∫ 0 h p ( y ) w d y ⋅ y = ∫ 0 h 2 ρ 0 g w y 3 d y = 8 ρ 0 g w h 4
Therefore a b = 4 ⋅ 8 = 3 2