Hypothetical Relativistic Oscillator

Rather than the solutions shown below, I will proceed with a Newtonian solution.

The force acting on the particle is given by the change in momentum:

$\displaystyle F = \frac{dp}{dt}$

When special relativity is factored in, time is dilated and the time observed in an outer reference frame (our reference frame) to compensate for the high velocity increasing towards the speed of light.

The linear momentum of the relativistic object in this case is:

$\displaystyle p = \frac{ \dot{x} }{ \sqrt{1- \dot{x}^2}}$

Taking the derivative with respect to time of the momentum, we have:

$\displaystyle \frac{dp}{dt} = \frac{1}{(1-\dot{x}^2)^{\frac{3}{2}}} \ddot{x}$

So the equation of motion of the particle becomes:

$\boxed{\displaystyle \frac{1}{(1-\dot{x}^2)^{\frac{3}{2}}} \ddot{x} = -kx}$

We can numerically solve the second order ODE above using the Runge-Kutta 4th Order. Code is shown below. Here are the graphs showing the speed of the particle according to the Classical and Relativistic model. One is right and the other isn't; the speed of light is exceeded in one:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

#4th order Runge-Kutta numerical solution of second order ODE

import math


time = 0
deltaT = 10**-7


#initial conditions

k = 10

u_1 = 0.4
u_2 = 0

def differentialEquation(t,x,xdot): #applying RK4 by splitting 2nd order ODE into 2 first order ODEs

    Alpha = 1/((1-(xdot**2))**1.5) #special relativity term

    return (-1*k*x)/(Alpha) #equation of motion


while u_2 <= 0: #iterate till velocity is zero ie. half of period

    #evaluating slope at various points


    k0 = deltaT*u_2
    L0 = deltaT*differentialEquation(time,u_1,u_2)

    k1 = deltaT*(u_2 + 0.5*L0)
    L1 = deltaT*differentialEquation(time + 0.5*deltaT, u_1 + 0.5*k0, u_2 + 0.5*L0)

    k2 = deltaT*(u_2 + 0.5*L1)
    L2 = deltaT*differentialEquation(time + 0.5*deltaT, u_1 + 0.5*k1, u_2 + 0.5*L1)

    k3 = deltaT*(u_2 + L2)
    L3 = deltaT*differentialEquation(time + deltaT, u_1 + k2, u_2 + L2)


    #RK4 approximation of values

    u_1 = u_1 + (1/6)*(k0 + 2*k1 + 2*k2 + k3)
    u_2 = u_2 + (1/6)*(L0 + 2*L1 + 2*L2 + L3)

    time += deltaT

print("Period of oscillation = " +str(2*time))

The Lagrangian is:

$\mathcal{L} = -m c^2 \sqrt{1 - \frac{\dot{x}^2}{c^2}} - \frac{1}{2} k (x - L_0)^2$

Plugging in numbers:

$\mathcal{L} = -\sqrt{1 - \dot{x}^2} - 5 (x - 0.1)^2$

Equation of motion:

$\frac{d}{dt} \frac{\partial{\mathcal{L}}}{\partial{\dot{x}}} = \frac{\partial{\mathcal{L}}}{\partial{x}}$

Evaluating results in:

$\ddot{x} = \frac{-10 (x - 0.1)}{\dot{x}^2 (1 - \dot{x}^2)^{-3/2} + (1 - \dot{x}^2)^{-1/2}}$

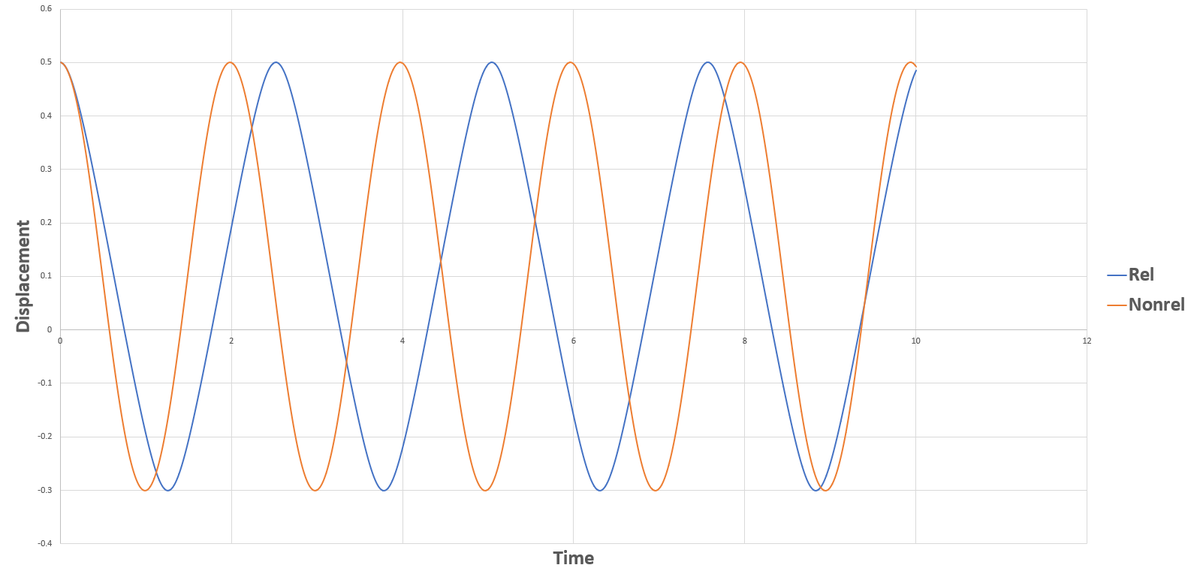
Note that at low speeds $(\dot{x}^2 << 1)$ , this expression reduces to just the numerator, which happens to be the classical Newton's 2nd Law. The period of a mass-spring oscillator is proportional to the square root of the mass, and relativistic particles behave as if they have more mass than classical particles. So we expect the period for the relativistic oscillator to be greater than that of the classical oscillator. The graph below demonstrates that behavior. Simulation code is also attached.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

import math

rel = 0

dt = 10.0**(-5.0)

x = 0.5
xd = 0.0
xdd = 0.0

t = 0.0
count = 0

xmax = 0.0

while t <= 10.0:

    x = x + xd*dt
    xd = xd + xdd*dt

    num = -10.0*(x-0.1)

    if rel == 1:

        q = (1.0-xd**2.0)**(-1.0/2.0)
        denom = (xd**2.0)*(q**3.0) + q
        xdd = num/denom

    else:
        xdd = num

    if (t>2.0) and (t<3.0) and (x>xmax):

        xmax = x
        t_store = t

    t = t + dt
    count = count + 1

    if count % 1000 == 0:
        print t,x

print ""
print ""
print dt
print t_store

Solving the equation of motion of the particle we get the following expression for the magnitude of velocity :

$v=\dfrac{dx}{dt}=\dfrac{1}{2mc}\sqrt {4mc^2k(x_0^2-x^2)-k^2(x_0^2-x^2)^2}=2\sqrt {10(0.25-x^2)-25(0.25-x^2)^2}$ .

Integrating this from $x=0$ to $x=x_0$ , we get one fourth of the time period as $\dfrac{T}{4}\approx 0.631$ . Hence the required time period is $\approx 4\times 0.631=\boxed {2.524}$ .