I already drew the graph!
How many of the given functions below can have the graph shown in the image?
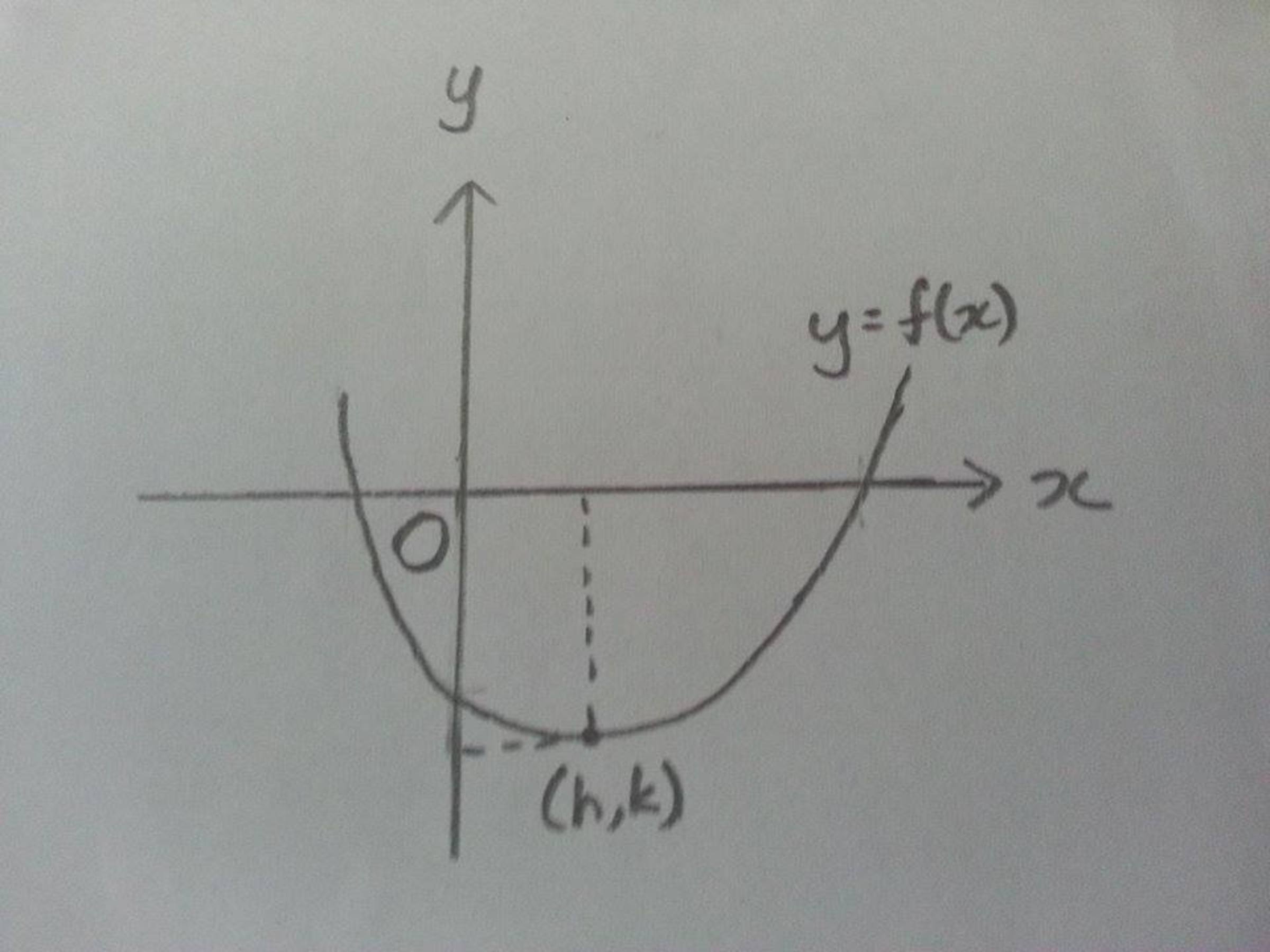
Details: is the minimum point of the graph
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Condition 1 : The graph in the image is a parabola curve, therefore the function should be quadratic.
Therefore, functions 1 and 5 do not satisfy this.
From here, all explanations will be based on the general form of the quadratic function f ( x ) = a x 2 + b x + c
Condition 2 : It is a u-shaped parabola, which means that the coefficient of x 2 is positive, that is, a > 0 .
Therefore, function 7 does not satisfy this too.
Condition 3 : We know that the y -intercept is below the x -axis, therefore the y -intercept is negative, that is, c < 0
Function 2 does not satisfy this condition.
We are now down to 3 possibilities left.
Condition 4 : Next, we need to ensure that the function has 2 different real roots, which translates to b 2 − 4 a c > 0
Function 3: b 2 − 4 a c = ( − 4 ) 2 − 4 ( 1 ) ( − 5 ) = 1 6 + 2 0 = 3 6 > 0
Function 4: b 2 − 4 a c = ( 4 ) 2 − 4 ( 1 ) ( − 5 ) = 1 6 + 2 0 = 3 6 > 0
Function 6: b 2 − 4 a c = ( − 8 ) 2 − 4 ( 4 ) ( − 2 1 ) = 6 4 + 3 3 6 = 4 0 0 > 0
Fun fact: The determinants for these 3 functions are all perfect squares, therefore their roots are all rational numbers
Condition 5 : Lastly, the minimum point is located in quadrant 4. The x -value of the minimum point is positive ( x > 0 ) , and the y -value of the minimum point is negative ( y < 0 ) . We need to check the minimum points of each function. Here, I will demonstrate 3 different methods to find the minimum value of a quadratic function.
Function 3 (Method 1):
For quadratic functions, the minimum point is defined as ( − 2 a b , f ( − 2 a b ) )
− 2 a b = − 2 ( 1 ) − 4 = 2 > 0
f ( − 2 a b ) = f ( 2 ) = 2 2 − 4 ( 2 ) − 5 = − 9 < 0
The minimum point is ( 2 , − 9 ) , and it satisfies Condition 5 .
Function 4 (Method 2):
For quadratic functions, you can complete the square and write it in the form of f ( x ) = a ( x − p ) 2 + q . The minimum/maximum point is then defined as ( p , q ) .
x 2 + 4 x − 5 = x 2 + 4 x + 4 − 4 − 5 = ( x + 2 ) 2 − 9
The minimum point is ( − 2 , − 9 ) , and the x -coordinate does not satisfy Condition 5 .
Function 6 (Method 3):
At minimum points, the first derivative, f ′ ( x ) = 0 and the second derivative, f ′ ′ ( x ) > 0
f ( x ) = 4 x 2 − 8 x − 2 1 f ′ ( x ) = 8 x − 8 f ′ ′ ( x ) = 8 > 0
We have shown that the critical point is a minimum point, now we need to find the coordinates of the minimum point.
f ′ ( x ) = 0 8 x − 8 = 0 8 x = 8 ⟹ x = 1 f ( 1 ) = 4 ( 1 2 ) − 8 ( 1 ) − 2 1 = − 2 5
The minimum point is ( 1 , − 2 5 ) , and it satisfies Condition 5 .
Therefore, function 3, f ( x ) = x 2 − 4 x − 5 and function 6, f ( x ) = 4 x 2 − 8 x − 2 1 can have the graph shown in the image in the question.
The answer is 2