I am back

First gif animation

Second gif animation

$k = 3$

$GE = 3k = 3(3) = 9$

$FE = 9 - 1 = 8$

By $AA \triangle DGF \sim \triangle EGA \Rightarrow$ as $\frac{AG}{GF}=\frac{AB}{DF}=3$ so $AB=3DF\Rightarrow FC=2DF$ .

$\triangle DFA \sim \triangle CFE \Rightarrow \frac{FC}{DF}=2=\frac{FE}{4}\therefore \boxed{FE=8}$

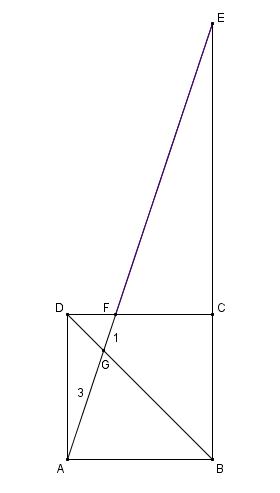Lets give the various points their coordinates A(0,0) B(x,0) C(x,x) D(0,x) where x is side of square Let angle FAB be y then G(3 cosy,3 siny) F(4 cos y ,4 sin y) Let AE =r therfore E(r cos y,r siny) As G lies on line DB therefore slope of line DG = slope of GB (3 siny - x)/(3cosy-0) = (3 siny)/(3 cosy - x) ........... eq(1) F lies on DC hence y coordinate of F will be same as that of D and C hence 4 siny = x ........ eq(2) Also the x coordinate of E will be same as that of B and C r cosy= x ........ eq(3) using eq(2) and Eq(3) we get r = 4 tan y ........eq(4) using eq(1) and eq(2) we get,on eliminating x, tan y = 3 therefore r=12. r = AF + FE AF = 4 therefore FE = 8