"I am Back" Says Integration Part 10
∫ 1 e [ ( e x ) x + ( x e ) x ] ln x d x = a e + e b
The equation above holds true for non-zero integers a and b . Find a + b .
Clarification:
e
≈
2
.
7
1
8
2
8
denotes the
Euler's number
.
The answer is 0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
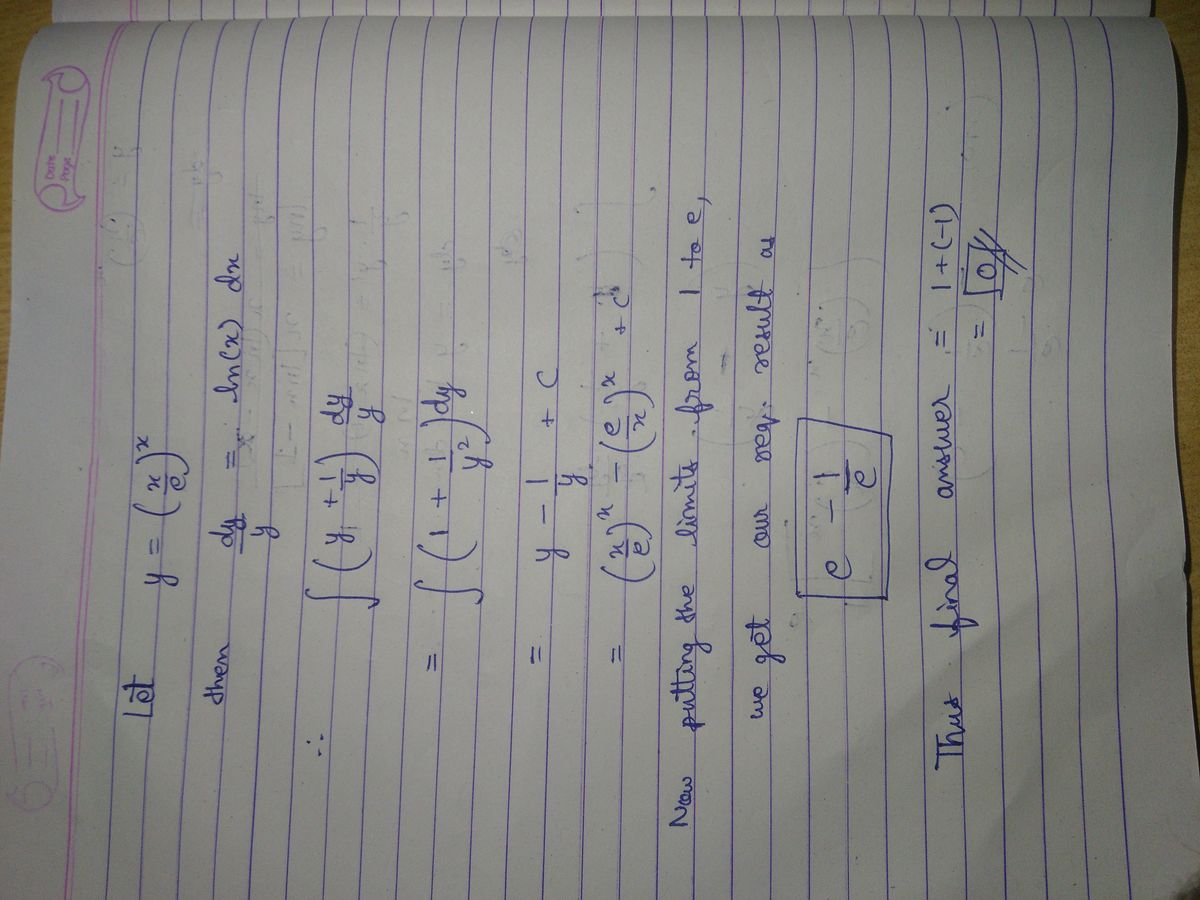
It is almost the same as mention[533040:Chew-Seong Cheong]'s Solution. And the way which I used to solve it.
Oh nice I just differentiated ( x / e ) x and found that the derivative is to be integrated in the question.
Log in to reply
I also did the same, just presented solution in diff manner.
I = ∫ 1 e [ ( e x ) x + ( x e ) x ] ln x d x = ∫ 1 e [ e x ( ln x − 1 ) + e − x ( ln x − 1 ) ] ln x d x = ∫ − 1 0 [ e u + e − u ] d u = e u − e − u ∣ ∣ ∣ ∣ − 1 0 = 1 − 1 − e − 1 + e 1 = e − e 1 Let u = x ( ln x − 1 ) , d u = ln x d x
⟹ a + b = 1 − 1 = 0
Rajdeep, we should use Brilliant.org's reference for Euler's number since it is available. I have amended the reference for you.
Log in to reply
Thank You , I couldn't find it on Brilliant at first so I added the Wikipedia one. Anyways Nice solution !
Log in to reply
Just enter the key words in the search box above.
bhaiya is ashish arora book good and enough for ipho and jee advanced