I am Groot!
A tree undergoes a sprouting growth.
Its longest branch is 32 units long, and the pair of branches connected to it are both 3 1 the length of that branch. The same pattern continues with the length consistently shortening by 3 1 in each step. Adjacent branches meet at 1 2 0 ∘ .
If this tree sprouts an infinite number of branches, what is its total height?
The answer is 42.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
15 solutions
and is that 32+7/6, or (32*7)/6?
The question was what is the total length, not what was the final height!!!!!
Log in to reply
The question asks for total height
Log in to reply
Hello Steven. Yes, I was too hasty in reading the question. I calculated the total length and was surprised that it was not the right answer. So, when I read the real solution, I was surprised that the answer calculated the height instead of the length. Thank you for your response.
We note that the height of the tree is given by:
H = 3 2 ( 1 + 3 1 cos 6 0 ∘ + ( 3 1 ) 2 + ( 3 1 ) 3 cos 6 0 ∘ + ( 3 1 ) 4 + ⋯ ) = 3 2 ( 1 + 3 1 × 2 1 + ( 3 1 ) 2 + ( 3 1 ) 3 × 2 1 + ( 3 1 ) 4 + ⋯ ) = 3 2 ( n = 0 ∑ ∞ ( 3 1 ) 2 n + 2 1 n = 0 ∑ ∞ ( 3 1 ) 2 n + 1 ) = 3 2 ( n = 0 ∑ ∞ ( 9 1 ) n + 6 1 n = 0 ∑ ∞ ( 9 1 ) n ) = 6 3 2 × 7 n = 0 ∑ ∞ ( 9 1 ) n = 6 3 2 × 7 × 1 − 9 1 1 = 6 3 2 × 7 × 8 9 = 4 2
Considering that the diagonal branch is one-third the length of its immediately preceding branch (which is vertical) and that it forms an angle of 1 2 0 ∘ with this vertical branch, it actually increases the tree's height by a factor of only sin 3 0 ∘ × 3 1 = 2 1 × 3 1 = 6 1 . Now the tree is 6 7 its original height with the diagonal branch. After the first diagonal branch, the tree's height grows to 3 2 × 6 7 = 3 1 1 2 .
Next we have another vertical branch and the cycle repeats itself. This vertical branch is 3 1 the length of the immediately preceding diagonal branch which means it is 3 1 × 3 1 = 9 1 the length of the immediately preceding vertical branch, so with each cycle, the tree's height increases by a factor of 9 1 . Employing infinite series, the tree's height will eventually be almost this tall:
3 1 1 2 ( 1 + 9 1 + 9 2 1 + . . . ) = 1 − 9 1 3 1 1 2 = 9 8 3 1 1 2 = 3 1 1 2 8 9 = 1 4 × 3 = 4 2 .
Let's start by working out the relative total height of the vertical lines. As each vertical line is 3 1 × 3 1 = 9 1 of the height of the previous vertical line, we can get the following infinite sum (where v is the height of the first line):
h v = v + 9 v + 9 2 v + 9 3 v + . . .
We can solve h v by first dividing both sides by 9 to get:
9 h v = 9 v + 9 2 v + 9 3 v + 9 4 v + . . .
Which we then substitute into the first series to get:
h v = v + 9 h v
Which we can rearrange to:
h v = v × 8 9
We now need to include the diagonals. With trigonometry, we can get the height of each diagonal with l e n g t h × cos ( 6 0 ) = l e n g t h × 2 1 . This shows that the height of each diagonal is 2 1 × 3 1 = 6 1 of the previous vertical line. By pairing up each diagonal with the previous vertical, we can see that the full height of the tree is 1 + 6 1 = 6 7 of the sum of the heights of all vertical lines ( h v ). From this, we can now work out:
h = h v × 6 7 = ( v × 8 9 ) × 6 7 = v × 1 6 2 1
By plugging in the initial 3 2 , we can get our final answer:
h = 3 2 × 1 6 2 1 = 4 2 .
Since the angles are equal to 1 2 0 ∘ , all are congruent and therefore every second branch will be parallel to the first one, and every other branch will form an angle of 3 0 ∘ degrees with the horizontal. Hence, we must add the heights of the vertical branches and the halves of the lengths of the remaining ones.
The length of the n th branch (0-indexed) is given by l n = 3 n 3 2 , and we should multiply each l n by either 2 1 or 1 , depending on its parity. Hence, we find the function f ( i ) which maps even values of i to 1 and odd ones to 2 :
f ( i ) = 2 ( − 1 ) i + 1 + 3
Now, we can simply plug all those values into a closed-form expression:
H = i = 0 ∑ ∞ ( 3 i ⋅ ( ( − 1 ) i + 1 + 3 ) 6 4 ) = 4 2
...kinda seems to me like f(i) maps odd values to 2 though.
I think you meant to put 1 instead of 3 in your first function.
The Ultimate Answer to Life, The Universe and Everything is...42
We classify the branches in two ways: vertical and at a 3 0 o angle. Notice, these alternately and consistently form the peak of the tree as we move from one step to another. Furthermore, the branches are multiplied by a factor of 3 1 each time, forming a geometric sequence of factor ( 3 1 ) 2 = 9 1 with these two types of branches. The first vertical branch is of length 3 2 , so its geometric series sums to 1 − 9 1 3 2 = 9 8 3 2 = 4 ⋅ 9 = 3 6 The first slanted branch has length 3 3 2 , and forms a 30-60-90 triangle with horizontal and vertical lines, equating to a height of sin 3 0 o ⋅ 3 3 2 = 2 1 ⋅ 3 3 2 = 3 1 6 . This means its geometric series sums to 1 − 9 1 3 1 6 = 9 8 3 1 6 = 3 1 6 ⋅ 8 9 = 6 So the total max height is 3 6 + 6 = 4 2
1/3 of 32 is 10.66, which round down to the next whole number of 10. The tree can only reach a height of of the starting plus 1/3 of height of longest branch of 32.
(0.33)32=10.66 10+32=42
First introduce two sequences:
v = ( v n ) n ≥ 0 gives the length of the n t h branch ( n starts at 0) and u = ( u n ) n ≥ 0 the gain in altitude of the n t h branch. (We consider only one path of branch, they are all equivalents).
It is easy to see that: ∀ n ≥ 0 , v n = 3 n 1 × 3 2 And: ∀ n ≥ 0 , u 2 n = v 2 n , u 2 n + 1 = 2 1 v 2 n + 1 because ∣ cos 1 2 0 ∘ ∣ = 2 1
We search this value (if it converges) n = 0 ∑ ∞ u n
Note that u and v are positive sequences, ∀ n ≥ 0 , v n ≥ u n and n ≥ 0 ∑ v n converges, it is a geometric series with r = 3 1 , ∣ r ∣ < 1 , thus n ≥ 0 ∑ u n converges let β its value ( β = n = 0 ∑ ∞ u n ) .
β = n = 0 ∑ ∞ u 2 n + n = 0 ∑ ∞ u 2 n + 1 = n = 0 ∑ ∞ 3 2 3 2 n 1 + n = 0 ∑ ∞ 1 6 3 2 n + 1 1
β = 3 2 n = 0 ∑ ∞ 9 n 1 + 3 1 6 n = 0 ∑ ∞ 9 n 1
∣ 9 1 ∣ < 1 so:
β = 1 − 9 1 1 ( 3 2 + 3 1 6 ) = 4 2
Therefore, the answer is 4 2
Similar to @Steven Chase 's solution
Relevant wiki: Sum of a Geometric Progression with Infinite Terms
Let the length of segment at stage n be l n
l 0 = 3 2 m
We know that l n + 1 = 3 1 l n
l n + 1 = ( 3 1 ) n + 1 l 0 ⇒ l n = ( 3 1 ) n l 0
Let the height at stage n be h n
h 0 = l 0 = 3 2 m
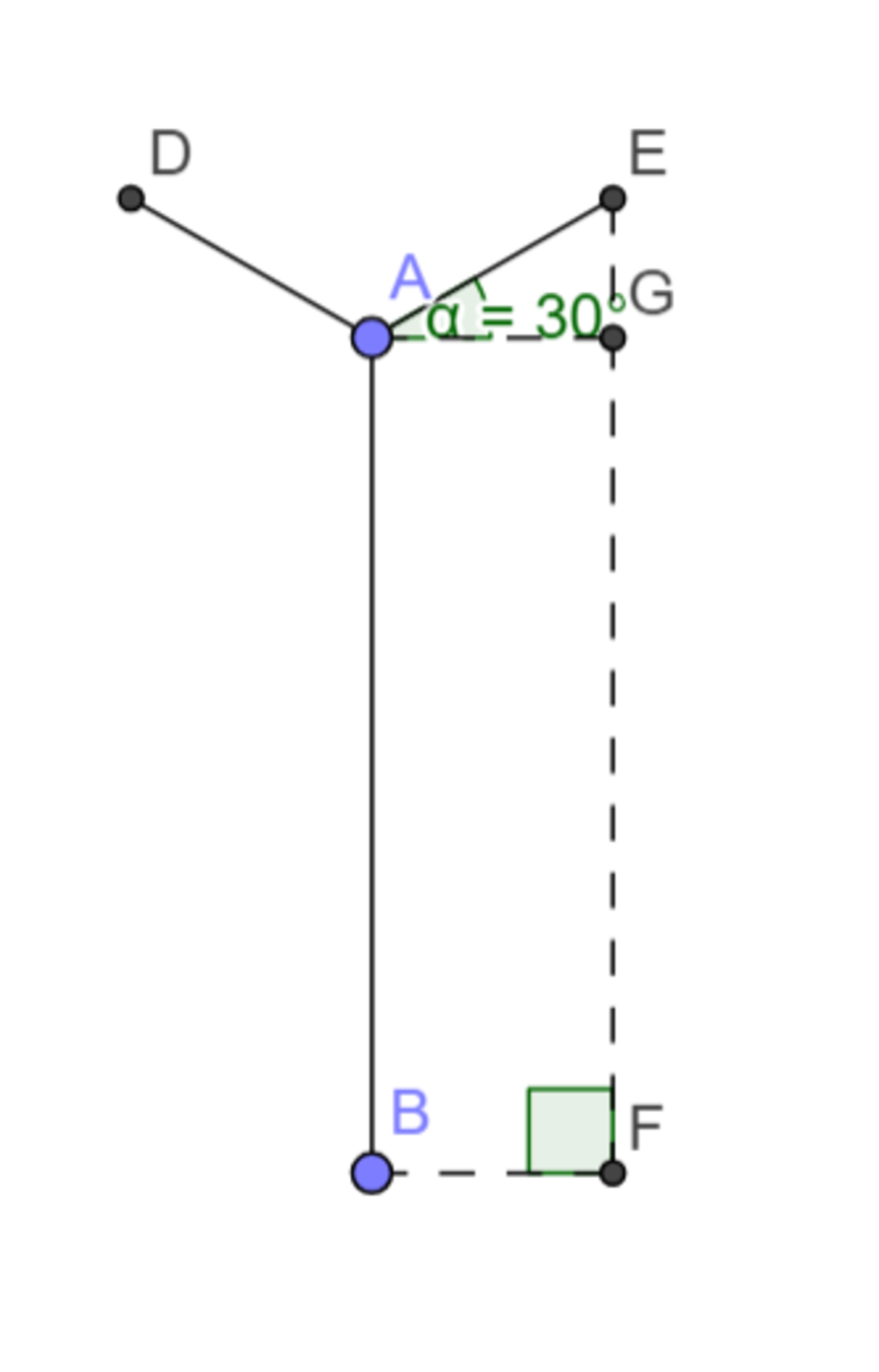
l 1 = 3 1 l 0 = 3 1 h 0
h 1 = h 0 + l 1 s i n 3 0 ∘ = h 0 + 3 1 l 0 s i n 3 0 ∘ = h 0 + 3 1 h 0 s i n 3 0 ∘ = h 0 + 3 1 h 0 ⋅ 2 1 = h 0 ( 1 + 6 1 )
h 2 = h 1 + l 2 = h 1 + ( 3 1 ) 2 l 0 = h 1 + ( 3 1 ) 2 h 0 = h 0 ( 1 + 6 1 + 9 1 )
h 3 = h 2 + l 3 s i n 3 0 ∘ = h 2 + ( 3 1 ) 3 l 0 ⋅ 2 1 = h 2 + ( 3 1 ) 3 h 0 ⋅ 2 1 = h 0 ( 1 + 6 1 + 9 1 + ( 3 1 ) 3 ⋅ 2 1 ) = h 0 ( 1 + 6 1 + 9 1 + 9 1 ⋅ 6 1 ) = h 0 ( 1 + 6 1 ) ( 1 + 9 1 )
∴ lim n → ∞ h n = h 0 ( 1 + 6 1 ) ( 1 + 9 1 + ( 9 1 ) 2 + . . . ) = h 0 ⋅ 6 7 ⋅ 1 − 9 1 1 = h 0 ⋅ 6 7 ⋅ 8 9 = 3 2 ⋅ 6 7 ⋅ 8 9 = 4 2 m
Each branch is 1/3 its previous, this means that the total length of one branch-line (the only one which moves constantly up - there are two, but identical) is a + a/3 + a/9 + a/27 + ... or a + a/3^1 + a/3^2 + a/3^3 +..., where a is the size of the starting branch. But each second branch is tilted in a way that 3 new branches are formed with an angle of 120deg to each other. This means that each second branch is a hypotenuse in a right-triangle whose height is x*sin(30deg) where x is the hypotenuse, as 120deg (angle diff) - 90deg (angle from vertical branch to horizontal line at 90deg to height) = 30deg. sin(30deg) = 1/2, so each second term of our infinite series has to be multiplied by 1/2.
So we get the series a + a/2 3 + a/9 + a/2 27 + ..., which can be "split" into the two following series:
a/2 + a/2 3 + a/2 9 + a/2 27 + ... = 1/2(a + a/3 + a/9 + a/27 + ...) and a/2 + a/2 9 + a/2 27 + a/2 243 + ... = 1/2(a + a/9 + a/27 + a/243 + ...)
These series are simple geometric series, each multiplied by 1/2. Solving each of the above geometric series yields 3a/2 and 9a/8, respectively. When you multiply by 1/2, you get 3a/4 and 9a/16. Adding these two sums (in order to get the sum of the original series back) yields 21a/16. As a is 32 (given by the problem), 21*32/16 yields 42.
First note that the "Y" portion of the tree repeats itself infinitely. The infinite sum of the height of the smaller getting "Y" portions converges which yields the height of the entire tree. Counting from the base branch with n = 0 all vertical parts of the "Y" portions are "even". Therefore their length can be described by ( 3 1 ) 2 n × 3 2 or ( 9 1 ) n × 3 2 . The length of the "odd" parts (the branches which are not vertical) is satisfied by the term ( 3 1 ) 2 n + 1 × 3 2 × cos 6 0 ∘ .
Hence, the height of the tree is given by the following term:
n = 0 ∑ ∞ ( 9 1 ) n × 3 2 + ( 3 1 ) 2 n + 1 × 3 2 × cos 6 0 ∘
= 3 2 n = 0 ∑ ∞ ( 9 1 ) n + ( 3 1 ) 2 n + 1 × cos 6 0 ∘
= 3 2 n = 0 ∑ ∞ ( 9 1 ) n + ( 3 1 ) 2 n + 1 × 2 1
= 3 2 n = 0 ∑ ∞ ( 9 1 ) n + 3 1 × ( 3 1 ) 2 n × 2 1
= 3 2 n = 0 ∑ ∞ ( 9 1 ) n + 6 1 × ( 3 1 ) 2 n
= 3 2 n = 0 ∑ ∞ ( 9 1 ) n + 6 1 × ( 3 1 × 3 1 ) n
= 3 2 n = 0 ∑ ∞ 6 6 × ( 9 1 ) n + 6 1 × ( 9 1 ) n
= 3 2 × 6 7 n = 0 ∑ ∞ ( 9 1 ) n = 6 3 2 × 7 × 1 − 9 1 1
= 3 2 × 7 6 × 8 9 = 6 × 8 3 2 × 7 × 9 = 4 8 3 2 × 6 3 = 3 2 × 6 3 = 3 1 2 6 = 4 2
The solution might seem too long at first glance, but this is solely due to the extremely detailed conversion!
This is a very diffiult problem on its own. But considering that the answer to the meaning of life, the universe and everything is always 42, the answer must be 42.
The answer to life the universe and everything is 42. This question is part of everything so the answer is 42. QED
Indexing terms starting at zero, the even terms will have vertical branches and odd terms will be off vertical by 30 degrees, so the effective height will be sin(30 deg) = 1/2.
Even terms are sum(32/3^(2k) for k in Natural Numbers) Odd terms are 1/2*sum(32/3^(2k+1) for k in Natural Numbers)
Simplifying, even=32*geom(1/9) where geom(x) = sum(x^k for k in Natural Numbers) = 1/(1-x) if abs(x)<1.
Odd = (32/2)(1/3) geom(1/9) =16/3 geom(1/9)
geom(1/9)=1/(1-1/9)=9/8
So total is (32)*(9/8) + (16/3)(9/8) = 36 + 6 = 42
So the vertical branches are responsible for a total height of 36, most of which comes from the initial branch of size 32. The cockeyed branches are responsible for a total height of 6.
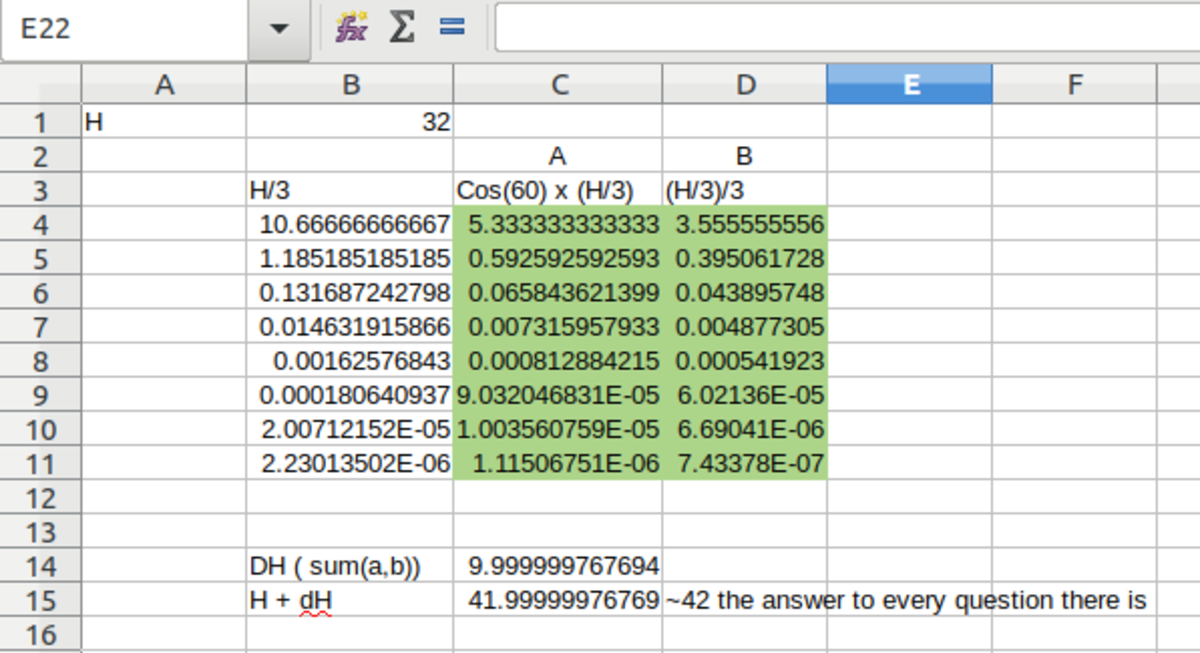
Solved using spreadsheet program. A indicates angled branches, B is vertical branches. Answer is 42, of-course.
The height of the first "Y" portion is:
H 1 = 3 2 ( 1 + 3 1 s i n ( 3 0 ∘ ) ) = 3 2 ( 1 + 3 1 2 1 ) = 3 2 6 7
Then the total height is based on an infinite geometric series with initial term H 1 and common ratio 9 1 :
H = 1 − 9 1 H 1 = 8 9 H 1 = 8 9 6 7 3 2 = 4 2